题目内容
已知椭圆 :
:
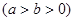 ,
,
(1)若椭圆的长轴长为4,离心率为 ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)在(1)的条件下,设过定点 的直线
的直线 与椭圆
与椭圆 交于不同的两点
交于不同的两点 ,且
,且 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线 的斜率
的斜率 的取值范围;
的取值范围;
(3)过原点 任意作两条互相垂直的直线与椭圆
任意作两条互相垂直的直线与椭圆 :
:
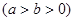 相交于
相交于 四点,设原点
四点,设原点 到四边形
到四边形 的一边距离为
的一边距离为 ,试求
,试求 时
时 满足的条件.
满足的条件.
【答案】
(1) ;(2)
;(2) ;(3)
;(3) .
.
【解析】
试题分析:(1)利用已知条件找出 解出
解出 、
、 即得;(2)设直线方程,联立方程组消去
即得;(2)设直线方程,联立方程组消去 得到关于
得到关于 的方程,由
的方程,由 求出
求出 的范围;(3)设直线
的范围;(3)设直线 的方程为
的方程为 联立方程组消去
联立方程组消去 到关于
到关于 的方程,利用
的方程,利用 、韦达定理、点到直线的距离公式求解.
、韦达定理、点到直线的距离公式求解.
试题解析:(1)依题意, ,解得
,解得 ,故椭圆
,故椭圆 的方程为
的方程为 .
.
(2)如图,依题意,直线 的斜率必存在,
的斜率必存在,

设直线 的方程为
的方程为 ,
, ,
, ,
,
联立方程组 ,消去
,消去 整理得
整理得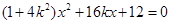 ,
,
由韦达定理, ,
, ,
,

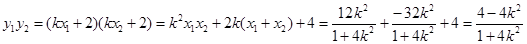 ,
,
因为直线 与椭圆
与椭圆 相交,则
相交,则 ,
,
即 ,解得
,解得 或
或 ,
,
当 为锐角时,向量
为锐角时,向量 ,则
,则 ,
,
即 ,解得
,解得 ,
,
故当 为锐角时,
为锐角时, .
.
如图,

依题意,直线 的斜率存在,设其方程为
的斜率存在,设其方程为 ,
, ,
, ,由于
,由于 ,
,

 ,即
,即 ,又
,又 ,
,

 ①
①
联立方程组 ,消去
,消去 得
得 ,
,
由韦达定理得 ,
, ,代入①得
,代入①得
 ,
,
令点 到直线
到直线 的距离为1,则
的距离为1,则 ,即
,即 ,
,

 ,
,
整理得 .
.
考点:椭圆的性质,直线与椭圆的位置关系.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
 如图,已知椭圆:
如图,已知椭圆: 如图,已知椭圆Γ:
如图,已知椭圆Γ: