题目内容
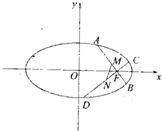 如图,已知椭圆:
如图,已知椭圆:| x2 |
| 25 |
| y2 |
| 9 |
(1)线段MN是否恒过一个定点?如果经过定点,试求出它的坐标,如果不经过定点,试说明理由;
(2)求分别以AB,CD为直径的两圆公共弦中点的轨迹方程.
分析:(1)设出直线AB的方程,代入椭圆方程消去x,设A,B的坐标,根据韦达定理可求得y1+y2的表达式,根据直线方程可求得x1+x2的表达式,进而可求得点M的坐标,根据AB⊥CD,将t换成-
,即可求得N的坐标,进而可求得MN的直线方程,把y=0代入直线方程求得x=
进而可推断出直线MN横过(
,0).
(2)根据(1)可表示出以AB为直径的圆的方程,进而依据AB⊥CD,将t换成-
,即可表示出直线CD的方程,两方程相减即可求得公共弦所在的方程,与直线MN方程联解消去t-
即可求得x和y的关系是,即以AB,CD为直径的两圆公共弦中点的轨迹方程.
| 1 |
| t |
| 50 |
| 17 |
| 50 |
| 17 |
(2)根据(1)可表示出以AB为直径的圆的方程,进而依据AB⊥CD,将t换成-
| 1 |
| t |
| 1 |
| t |
解答:解:(1)设直线AB的方程为:x=ty+4,代入
+
=1并整理得:
(9t2+25)y2+72ty-81=0.
设A(x1,y1),B(x2,y2),则有:y1+y2=-
,x1+x2=t(y1+y2)+8=
,
所以点M(
,
)
∵AB⊥CD,
∴将t换成-
,即得:N(
,
).
由两点式得直线MN的方程为x-
(t-
)y=
.
当y=0时,x=
,所以直线MN恒过定点(
,0).
(2)以弦AB为直径的圆M的方程为:x2+y2-
x+
y+
=0①
又∵AB⊥CD,
∴将t换成-
,即得以弦CD为直径的圆N的方程为:x2+y2-
x-
y+
=0.②
①-②得两圆公共弦所在直线方程为:25x+
-118=0.③
又直线MN的方程为:x-
(t-
)y=
.④
联解③④,消去t-
,得两圆公共弦中点的轨迹方程为:(x-
)(x-
)+y2=0.
其轨迹是过定点(
,0)的圆.
| x2 |
| 25 |
| y2 |
| 9 |
(9t2+25)y2+72ty-81=0.
设A(x1,y1),B(x2,y2),则有:y1+y2=-
| 72t |
| 9t2+25 |
| 200 |
| 9t2+25 |
所以点M(
| 100 |
| 9t2+25 |
| 36t |
| 9t2+25 |
∵AB⊥CD,
∴将t换成-
| 1 |
| t |
| 100t2 |
| 9+25t2 |
| 36t |
| 9+25t2 |
由两点式得直线MN的方程为x-
| 25 |
| 34 |
| 1 |
| t |
| 50 |
| 17 |
当y=0时,x=
| 50 |
| 17 |
| 50 |
| 17 |
(2)以弦AB为直径的圆M的方程为:x2+y2-
| 200 |
| 9t2+25 |
| 72t |
| 9t2+25 |
| 319-225t2 |
| 9t2+25 |
又∵AB⊥CD,
∴将t换成-
| 1 |
| t |
| 200t2 |
| 9+25t2 |
| 72t |
| 9+25t2 |
| 319t2-225 |
| 9+25t2 |
①-②得两圆公共弦所在直线方程为:25x+
| 17 | ||
t-
|
又直线MN的方程为:x-
| 25 |
| 34 |
| 1 |
| t |
| 50 |
| 17 |
联解③④,消去t-
| 1 |
| t |
| 50 |
| 17 |
| 118 |
| 25 |
其轨迹是过定点(
| 50 |
| 17 |
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了考生分析推理和基本的运算能力.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目

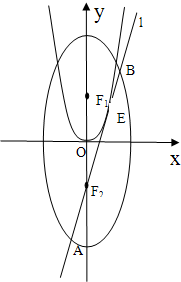 如图,已知椭圆
如图,已知椭圆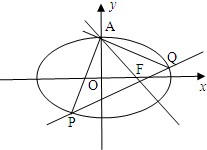 (2012•梅州一模)如图,已知椭圆C:
(2012•梅州一模)如图,已知椭圆C: (2003•北京)如图,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0
(2003•北京)如图,已知椭圆的长轴A1A2与x轴平行,短轴B1B2在y轴上,中心M(0,r)(b>r>0 如图,已知椭圆C:
如图,已知椭圆C: