题目内容
【题目】已知椭圆M： 
=1（a＞b＞0）的离心率为 
，左焦点F1到直线 
的距离为3，圆N的方程为（x﹣c）2+y2=a2+c2（c为半焦距），直线l：y=kx+m（k＞0）与椭圆M和圆N均只有一个公共点，分别设为A，B．
（1）求椭圆M的方程和直线l的方程；
（2）在圆N上是否存在点P，使 
，若存在，求出P点坐标，若不存在，说明理由．
【答案】
（1）解：∵椭圆M： 
=1（a＞b＞0）的离心率为 
，左焦点F1到直线 
的距离为3，
∴由题意知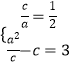 
，解得a=2，c=1．
∴b= 
= 
，
∴椭圆M的方程为 
+ 
=1，
圆N的方程为（x﹣1）2+y2=5，
∵直线l：y=kx+m（k＞0）与椭圆M只有一个公共点，
∴由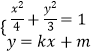 
，得（3+4k2）x2+8kmx+4m2﹣12=0，①
∴△=64k2m2﹣4（3+4k2）（4m2﹣12）=0，
整理得m2=3+4k2，②
由直线l：y=kx+m与N只有一个公共点，得 
= 
，即k2+2km+m2=5+5k2，③
将②代入③得km=1，④由②④得k= ，m=2．
∴直线l：y= x+2．
（2）将k= ，m=2代入①可得A（﹣1， 
），
又过切点B的半径所在的直线l′：y=﹣2x+2，
与直线l的方程联立得B（0，2），
设P（x0，y0），由 
=2 
，得 
，
化简得7 
+7 
+16x0﹣20y0+22=0，⑤
又P（x0，y0）满足 
=4，⑥
将⑤﹣7×⑥并整理得3x0﹣2y0+5=0，
即y0= 
，⑦
将⑦代入⑥并整理得13 +22x0+9=0，
解得x0=﹣1或x0=﹣ 
，
所以存在P（﹣1，1）或P（﹣ ， 
）满足条件．
【解析】（1）由椭圆的离心率为 ，左焦点F1到直线 的距离为3，列出方程组，求出a，b，由此能求出椭圆M的方程；由 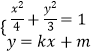，得（3+4k2）x2+8kmx+4m2﹣12=0，由此利用根的判别式、点到直线距离公式能求出直线l的方程．（2）将k= ，m=2代入，得A（﹣1， ），过切点B的半径所在的直线l′：y=﹣2x+2，与直线l的方程联立得B（0，2），设P（x0，y0），由 =2 ，得7 +7 +16x0﹣20y0+22=0，再由P（x0，y0）满足 =4，能求出存在P（﹣1，1）或P（﹣ ， ）满足条件．
