题目内容
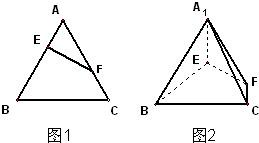
在正三角形ABC中,E、F、P分别是AB、AC、BC边上的点,满足AE:EB=CF:FA=CP:PB=1:2(如图1).将△AEF沿EF折起到△A1EF的位置,使二面角A1-EF-B成直二面角,连接A1B、A1P(如图2)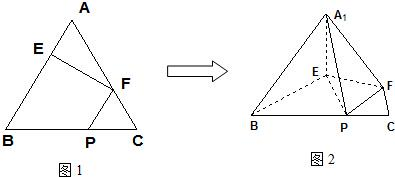
(Ⅰ)求证:A1E⊥平面BEP;
(Ⅱ)求直线A1E与平面A1BP所成角的大小;
(Ⅲ)求二面角B-A1P-F的大小(用反三角函数表示).
分析:本小题主要考查线面垂直、直线和平面所成的角、二面角等基础知识,以及空间线面位置关系的证明、角和距离的计算等,考查空间想象能力、逻辑推理能力和运算能力.
解答: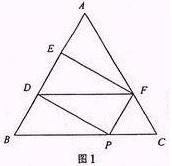 解:解法一:不妨设正三角形ABC的边长为3
解:解法一:不妨设正三角形ABC的边长为3
(1)在图1中,取BE中点D,连接DF.AE:EB=CF:FA=1:2
∴AF=AD=2而∠A=60°,
∴△ADF是正三角形,又AE=DE=1,
∴EF⊥AD在图2中,A1E⊥EF,BE⊥EF,
∴∠A1EB为二面角A1-EF-B的平面角.由
题设条件知此二面角为直二面角,A1E⊥BE,又BE∩EF=E(2)
∴A1E⊥平面BEF,
即A1E⊥平面BEP
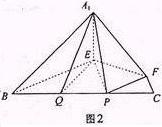 (3)在图2中,A1E不垂直A1B,
(3)在图2中,A1E不垂直A1B,
∴A1E是平面A1BP的垂线,又A1E⊥平面BEP,
∴A1E⊥BE.
从而BP垂直于A1E在平面A1BP内的射影(三垂线定理的逆定理)设A1E在平面A1BP内的射影为A1Q,且A1Q交BP于点Q,则∠E1AQ就是A1E与平面A1BP所成的角,且BP⊥A1Q.
在△EBP中,BE=EP=2而∠EBP=60°,
∴△EBP是等边三角形.又A1E⊥平面BEP,
∴A1B=A1P,
∴Q为BP的中点,且EQ=
,又A1E=1,
在Rt△A1EQ中,tan∠EA1Q=
=
,
∴∠EA1Q=60°,
∴直线A1E与平面A1BP所成的角为60°
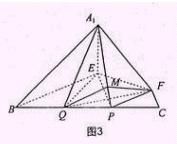 在图3中,过F作FM⊥A1P与M,连接QM,QF,
在图3中,过F作FM⊥A1P与M,连接QM,QF,
∵CP=CF=1,∠C=60°,
∴△FCP是正三角形,
∴PF=1.有PQ=
BP=1
∴PF=PQ①,
∵A1E⊥平面BEP,EQ=EF=
∴A1E=A1Q,
∴△A1FP≌△A1QP从而∠A1PF=∠A1PQ②,
由①②及MP为公共边知△FMP≌△QMP,
∴∠QMP=∠FMP=90°,且MF=MQ,
从而∠FMQ为二面角B-A1P-F的平面角.
在Rt△A1QP中,A1Q=A1F=2,PQ=1,又∴A1P=
.
∵MQ⊥A1P,∴MQ=
=
∴MF=
在△FCQ中,FC=1,QC=2,∠C=60°,由余弦定理得QF=
在△FMQ中,cos∠FMQ=
=-
∴二面角B-A1P-F的大小为π-arccos
 解:解法一:不妨设正三角形ABC的边长为3
解:解法一:不妨设正三角形ABC的边长为3(1)在图1中,取BE中点D,连接DF.AE:EB=CF:FA=1:2
∴AF=AD=2而∠A=60°,
∴△ADF是正三角形,又AE=DE=1,
∴EF⊥AD在图2中,A1E⊥EF,BE⊥EF,
∴∠A1EB为二面角A1-EF-B的平面角.由
题设条件知此二面角为直二面角,A1E⊥BE,又BE∩EF=E(2)
∴A1E⊥平面BEF,
即A1E⊥平面BEP
 (3)在图2中,A1E不垂直A1B,
(3)在图2中,A1E不垂直A1B,∴A1E是平面A1BP的垂线,又A1E⊥平面BEP,
∴A1E⊥BE.
从而BP垂直于A1E在平面A1BP内的射影(三垂线定理的逆定理)设A1E在平面A1BP内的射影为A1Q,且A1Q交BP于点Q,则∠E1AQ就是A1E与平面A1BP所成的角,且BP⊥A1Q.
在△EBP中,BE=EP=2而∠EBP=60°,
∴△EBP是等边三角形.又A1E⊥平面BEP,
∴A1B=A1P,
∴Q为BP的中点,且EQ=
| 3 |
在Rt△A1EQ中,tan∠EA1Q=
| EQ |
| A1E |
| 3 |
∴∠EA1Q=60°,
∴直线A1E与平面A1BP所成的角为60°
 在图3中,过F作FM⊥A1P与M,连接QM,QF,
在图3中,过F作FM⊥A1P与M,连接QM,QF,∵CP=CF=1,∠C=60°,
∴△FCP是正三角形,
∴PF=1.有PQ=
| 1 |
| 2 |
∴PF=PQ①,
∵A1E⊥平面BEP,EQ=EF=
| 3 |
∴A1E=A1Q,
∴△A1FP≌△A1QP从而∠A1PF=∠A1PQ②,
由①②及MP为公共边知△FMP≌△QMP,
∴∠QMP=∠FMP=90°,且MF=MQ,
从而∠FMQ为二面角B-A1P-F的平面角.
在Rt△A1QP中,A1Q=A1F=2,PQ=1,又∴A1P=
| 5 |
∵MQ⊥A1P,∴MQ=
| A1Q•PQ |
| A1P |
2
| ||
| 5 |
∴MF=
2
| ||
| 5 |
在△FCQ中,FC=1,QC=2,∠C=60°,由余弦定理得QF=
| 3 |
在△FMQ中,cos∠FMQ=
| MF2+MQ2-QF2 |
| 2MF•MQ |
| 7 |
| 8 |
∴二面角B-A1P-F的大小为π-arccos
| 7 |
| 8 |
点评:在立体几何学习中,我们要多培养空间想象能力,对于图形的翻折问题,关健是利用翻折前后的不变量,二面角的平面角的适当选取是立体几何的核心考点之一.是高考数学必考的知识点之一.作,证,解,是我们求二面角的三步骤.作:作出所要求的二面角,证:证明这是我们所求二面角,并将这个二面角进行平面化,置于一个三角形中,最好是直角三角形,利用我们解三角形的知识求二面角的平面角.向量的运用也为我们拓宽了解决立体几何问题的角度,不过在向量运用过程中,要首先要建系,建系要建得合理,最好依托题目的图形,坐标才会容易求得.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 在正三角形ABC中,E、F分别是AB、AC边上的点,满足
在正三角形ABC中,E、F分别是AB、AC边上的点,满足 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( )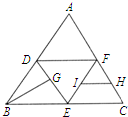 如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将
如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将