题目内容
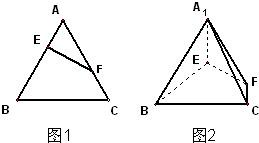 在正三角形ABC中,E、F分别是AB、AC边上的点,满足
在正三角形ABC中,E、F分别是AB、AC边上的点,满足| AE |
| EB |
| CF |
| FA |
| 1 |
| 2 |
分析:不妨设正三角形ABC的边长为3,在图1中取BE中点D,连接DF,根据
=
=
,求出AE=1,AF=2而∠A=60°,EF⊥AE,在图2中有A1E⊥EF,BE⊥EF,根据二面角的平面角的定义可知∠A1EB为二面角A1-EF-B的平面角,而二面角A1-EF-B为直二面角,则A1E⊥BE
又BE∩EF=E,满足线面垂直的判定定理,则A1E⊥平面BEC.
| AE |
| EB |
| CF |
| FA |
| 1 |
| 2 |
又BE∩EF=E,满足线面垂直的判定定理,则A1E⊥平面BEC.
解答:证明:不妨设正三角形ABC的边长为3,则
在图1中,取BE中点D,连接DF,
则∵
=
=
,
∴AE=1,AF=2而∠A=60°,∴EF⊥AE
∴在图2中有A1E⊥EF,BE⊥EF,
∴∠A1EB为二面角A1-EF-B的平面角
∵二面角A1-EF-B为直二面角,∴A1E⊥BE
又∵BE∩EF=E,∴A1E⊥平面BEC.
在图1中,取BE中点D,连接DF,
则∵
| AE |
| EB |
| CF |
| FA |
| 1 |
| 2 |
∴AE=1,AF=2而∠A=60°,∴EF⊥AE
∴在图2中有A1E⊥EF,BE⊥EF,
∴∠A1EB为二面角A1-EF-B的平面角
∵二面角A1-EF-B为直二面角,∴A1E⊥BE
又∵BE∩EF=E,∴A1E⊥平面BEC.
点评:本题主要考查了直线与平面垂直的判定,以及二面角的应用等有关知识,同时考查了空间想象能力、推理论证能力,属于中档题.

练习册系列答案
相关题目
 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,J分别为AF,DE的中点.将△ABC沿DE,EF,DF折成三棱锥以后,GJ与DE所成角的度数为( ) 如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将
如图,在正三角形ABC中,D,E,F分别为AB,BC,AC的中点,G,H,I分别为DE,FC,EF的中点,将