题目内容
如图，在正三角形ABC中，D，E，F分别为各边的中点，G，J分别为AF，DE的中点．将△ABC沿DE，EF，DF折成三棱锥以后，GJ与DE所成角的度数为（ ）分析：先画出翻折后的图形，然后连接DG、GE，然后根据三棱锥为正四面体可得DG=GE，点J为DE的中点，则GJ⊥DE，从而求出所求．
解答：解：连接DG、GE，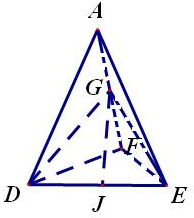
根据题意可知三棱锥为正四面体
点G为AF的中点，则DG=GE
而点J为DE的中点，则GJ⊥DE
∴GJ与DE所成角的度数为90°
故选A．
根据题意可知三棱锥为正四面体
点G为AF的中点，则DG=GE
而点J为DE的中点，则GJ⊥DE
∴GJ与DE所成角的度数为90°
故选A．
点评：本题主要考查了两直线所成角，解题的关键就是弄清翻折后的图形，属于基础题．
练习册系列答案
相关题目
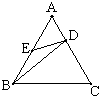如图，在正三角形ABC中，D、E分别在AC、AB上，| AD |
| AC |
| 1 |
| 3 |
| A、△AED∽△BED |
| B、△AED∽△CBD |
| C、△AED∽△ABD |
| D、△BAD∽△BCD |
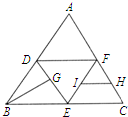如图，在正三角形ABC中，D，E，F分别为AB，BC，AC的中点，G，H，I分别为DE，FC，EF的中点，将
B．arccos
C．
D．arccos
