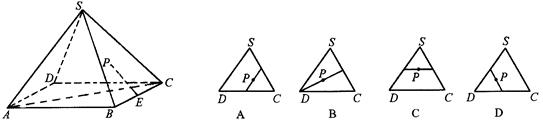
题目内容
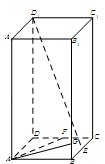
(本题满分12分)如图,在长方体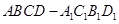 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱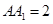 ,为
,为 中点,
中点,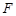 为
为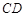 中点,
中点,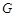 为
为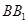 上一个动点.
上一个动点.
(Ⅰ)确定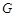 点的位置,使得
点的位置,使得 ;
;
(Ⅱ)当 时,求二面角
时,求二面角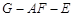 的平
的平
面角余弦值.
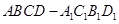 中,已知上下两底面为正方形,且边长均为1;侧棱
中,已知上下两底面为正方形,且边长均为1;侧棱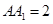 ,为
,为 中点,
中点,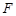 为
为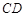 中点,
中点,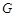 为
为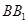 上一个动点.
上一个动点.
(Ⅰ)确定
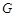 点的位置,使得
点的位置,使得 ;
;(Ⅱ)当
 时,求二面角
时,求二面角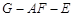 的平
的平面角余弦值.
(1)根据已知中的线线垂直关系, 来结合线面垂直的判定定理来分析线面垂直,这类试题先是猜想点的位置,然后加以证明。
(2)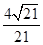
(2)
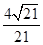
试题分析:方法一:
(Ⅰ)如图,
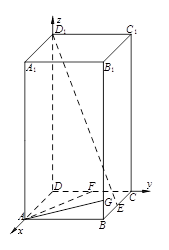
分别以
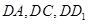 所在直线为
所在直线为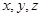 轴建立空间直角坐标系
轴建立空间直角坐标系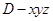 ,则
,则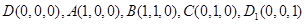
易得
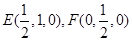 ………………2分
………………2分由题意得
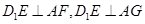 ,设
,设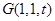
又
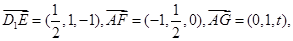
则由
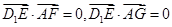 得
得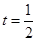 ,
,∴
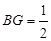 ,得
,得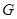 为
为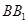 的四等分点.………………………6分
的四等分点.………………………6分(Ⅱ)易知平面
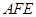 的一个法向量为
的一个法向量为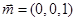 ,设平面
,设平面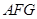 的法向量为
的法向量为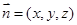
则
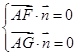 ,得
,得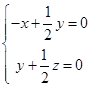 ,取
,取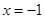 ,得
,得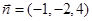 , ……………10分
, ……………10分∴
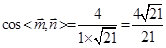 ,∴二面角
,∴二面角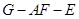 的平面角余弦值为
的平面角余弦值为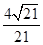 .12分
.12分方法二:
(Ⅰ)∵
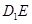 在平面
在平面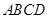 内的射影为
内的射影为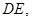 ,且四边形
,且四边形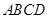 为正方形,
为正方形,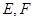 为中点, ∴
为中点, ∴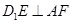
同理,
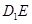 在平面
在平面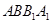 内的射影为
内的射影为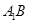 ,则
,则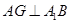
由△
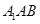 ~△
~△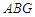 , ∴
, ∴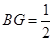 ,得
,得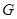 为
为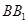 的四等分点. …………………6分
的四等分点. …………………6分(Ⅱ)∵
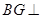 平面
平面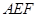 ,过
,过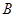 点作
点作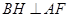 ,垂足为
,垂足为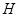 ;
;连结
 ,则
,则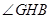 为二面角
为二面角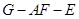 的平面角;…………………………8分
的平面角;…………………………8分由
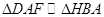 ,得
,得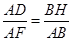 ,解得
,解得
∴在
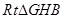 中,
中,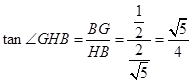 ,
,∴
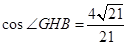 ;∴二面角
;∴二面角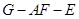 的平面角余弦值为
的平面角余弦值为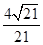 . …12分
. …12分点评:解决该试题的关键是能合理的根据结论 ,逆向求点点M的位置,进而结合向量法或者是几何性质法求解二面角,属于中档题。

练习册系列答案
相关题目
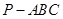 中,
中, 面
面 ,
, 是直角三角形,
是直角三角形, ,
, ,
, ,点
,点 分别为
分别为 的中点。
的中点。
 ;
; 与平面
与平面 所成的角的大小;
所成的角的大小; 的正切值。
的正切值。 平面ABC,
平面ABC, ,给出下列结论:①
,给出下列结论:① ;②平面
;②平面 平面PBC;③直线
平面PBC;③直线 平面PAE;④
平面PAE;④ ;⑤直线PD与平面PAB所成角的余弦值为
;⑤直线PD与平面PAB所成角的余弦值为 。
。

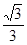


 、
、 ,能判定
,能判定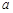

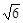 ,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记
,高CD=3,点E是线段BD上异于点B、D的动点.点F在BC边上,且EF⊥AB.现沿EF将△BEF折起到△PEF的位置,使PE⊥AE.记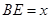 ,用
,用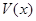 表示四棱锥P-ACFE的体积.
表示四棱锥P-ACFE的体积.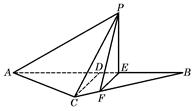
 中,底面
中,底面 是边长为2的正方形,
是边长为2的正方形, ,且
,且 ,
, 为
为 中点.
中点.
 平面
平面 的余弦值.
的余弦值. ,给定以下条件:
,给定以下条件: 内不共线的三点到
内不共线的三点到 的距离相等;②
的距离相等;② 是
是 ;
; ;
; 的是( )
的是( )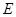 是
是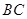 的中点,P点在侧面△SCD内及其边界上运动,并且总是保持
的中点,P点在侧面△SCD内及其边界上运动,并且总是保持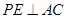 .则动点
.则动点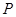 的轨迹与△
的轨迹与△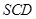 组成的相关图形最有可有是图中的( )
组成的相关图形最有可有是图中的( )