题目内容
7.已知M是焦点为F1(-1,0),F2(1,0)椭圆上任-点.且三角形F1MF2的面积的最大值$\sqrt{3}$.(1)求椭圆C的标准方程;
(2)一直线l过F2且与椭圆C交于A、B两点,交y轴于点P,证明:$\frac{|PB|}{|B{F}_{2}|}$-$\frac{|PA|}{|A{F}_{2}|}$为定值.
分析 (1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),由题意得c=1,由三角形的面积公式及椭圆的范围可得b=$\sqrt{3}$,由a,b,c的关系可得a,进而得到椭圆的方程;
(2)设直线l的方程为y=k(x-1),代入椭圆方程,设A(x1,y1),B(x2,y2),运用韦达定理,由$\frac{|PB|}{|B{F}_{2}|}$-$\frac{|PA|}{|A{F}_{2}|}$=$\frac{{x}_{2}-0}{1-{x}_{2}}$-$\frac{{x}_{1}}{{x}_{1}-1}$,化简整理即可得到定值.
解答 解:(1)设椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
由题意得c=1,三角形F1MF2的面积为$\frac{1}{2}$|yM|•2c=|yM|,
由椭圆的范围可得|yM|≤b,即有最大值为b=$\sqrt{3}$,
则a=$\sqrt{{b}^{2}+{c}^{2}}$=2,即有椭圆的标准方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)证明:设直线l的方程为y=k(x-1),代入椭圆方程可得,
(3+4k2)x2-8k2x+4k2-12=0,
设A(x1,y1),B(x2,y2),
即有x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$,x1x2=$\frac{4{k}^{2}-12}{3+4{k}^{2}}$,
又P(0,-k),F2(1,0),
即有$\frac{|PB|}{|B{F}_{2}|}$-$\frac{|PA|}{|A{F}_{2}|}$=$\frac{{x}_{2}-0}{1-{x}_{2}}$-$\frac{{x}_{1}}{{x}_{1}-1}$=$\frac{{x}_{1}+{x}_{2}-2{x}_{1}{x}_{2}}{{x}_{1}{x}_{2}+1-({x}_{1}+{x}_{2})}$
=$\frac{8{k}^{2}-2(4{k}^{2}-12)}{4{k}^{2}-12+3+4{k}^{2}-8{k}^{2}}$=-$\frac{8}{3}$.
即$\frac{|PB|}{|B{F}_{2}|}$-$\frac{|PA|}{|A{F}_{2}|}$为定值.
点评 本题考查椭圆的方程的求法,注意椭圆的范围的运用,考查直线和椭圆方程的联立,运用韦达定理,以及化简整理的能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案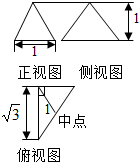 某几何体的三视图如图所示,则它的外接球的体积为( )
某几何体的三视图如图所示,则它的外接球的体积为( )| A. | 4π | B. | $\frac{8}{3}π$ | C. | $\frac{4}{9}π$ | D. | $\frac{4}{3}π$ |
| A. | -2 | B. | {2} | C. | {-2} | D. | 2∈A |