Question

（本小题满分14分）

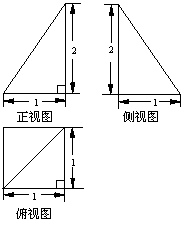
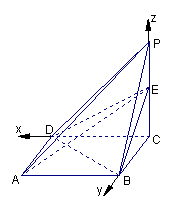
已知一个四棱锥P－ABCD的三视图如下，E是侧棱PC上的动点。

（1）求四棱锥P－ABCD的体积；

（2）是否不论点E在何位置，都有BD⊥AE？证明你的结论;

（3）若点E为PC的中点，求二面角D－AE－B的大小．

Answer 1

（1）解：由该四棱锥的三视图可知，该四棱锥P－ABCD的底面是边长为1的正方形，

侧棱PC⊥底面ABCD，且PC=2. ----------------------

-------2分

∴----------------------------4分

(2) 不论点E在何位置，都有BD⊥AE---------------------------------------5分

证明如下：连结AC，∵ABCD是正方形

∴BD⊥AC ∵PC⊥底面ABCD 且BD平面ABCD　∴BD⊥PC------7分

又∵∴BD⊥平面PAC　

∵不论点E在何位置，都有AE平面PAC 

∴不论点E在何位置，都有BD⊥AE ----------------------------10分

(3) 解法1：在平面DAE内过点D作DG⊥AE于G，连结BG

∵CD=CB,EC=EC, ∴Rt△ECD≌Rt△ECB

∴ED=EB, ∵AD=AB  ∴△EDA≌△EBA

∴BG⊥EA ∴∠DGB为二面角D－EA－B的平面角---------------12分

∵BC⊥DE,   AD∥BC  ∴AD⊥DE

在Rt△ADE中==BG

在△DGB中，由余弦定理得

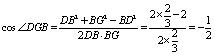∴∠DGB = …..14分

[解法２：以点C为坐标原点，CD所在的直线为ｘ轴建立空间直角坐标系如图示：

则,从而 

设平面ADE和平面ABE的法向量分别为m=(a,b,c),n=

由法向量的性质可得：，

令，则，∴m=(1,0,1),n=(0,-1,-1) ------13分

设二面角D－AE－B的平面角为θ，则 , ∴