题目内容
(2013•温州一模)设A(1,-1),B(0,1),若直线ax+by=1与线AB(包括端点)有公共点,则a2+b2的最小值为( )
分析:由题意得:点A(1,-1),B(0,1)在直线ax+by=1的两侧,那么把这两个点代入ax+by-1,乘积小于等于0,即可得出关于a,b的不等关系,画出此不等关系表示的平面区域,结合线性规划思想求出a2+b2的取值范围.
解答: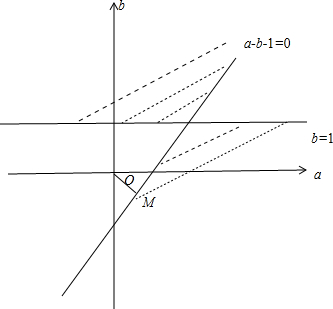 解:∵直线ax+by=1与线段AB有一个公共点,
解:∵直线ax+by=1与线段AB有一个公共点,
∴点A(1,-1),B(0,1)在直线ax+by=1的两侧,
∴(a-b-1)(b-1)≤0,
或
画出它们表示的平面区域,如图所示.
a2+b2表示原点到区域内的点的距离的平方,
由图可知,当原点O到直线a-b-1=0的距离为原点到区域内的点的距离的最小值,
∵d=
=
,
那么a2+b2的最小值为
故选C
 解:∵直线ax+by=1与线段AB有一个公共点,
解:∵直线ax+by=1与线段AB有一个公共点,∴点A(1,-1),B(0,1)在直线ax+by=1的两侧,
∴(a-b-1)(b-1)≤0,
|
|
画出它们表示的平面区域,如图所示.
a2+b2表示原点到区域内的点的距离的平方,
由图可知,当原点O到直线a-b-1=0的距离为原点到区域内的点的距离的最小值,
∵d=
| |-1| | ||
|
| ||
| 2 |
那么a2+b2的最小值为
| 1 |
| 2 |
故选C
点评:本题考查二元一次不等式组与平面区域问题、函数的最值及其几何意义,是基础题.准确把握点与直线的位置关系,找到图中的“界”,是解决此类问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC. (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC,
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC,