题目内容
 (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.(Ⅰ)求证:PA∥平面QBC;
(Ⅱ)PQ⊥平面QBC,求二面角Q-PB-A的余弦值.
分析:(Ⅰ)利用线面垂直的性质定理及线面平行的判定定理即可证明;
(Ⅱ)方法一:利用三角形的中位线定理及二面角的平面角的定义即可求出.
方法二:通过建立空间直角坐标系,利用平面的法向量所成的夹角来求两平面的二面角的平面角.
(Ⅱ)方法一:利用三角形的中位线定理及二面角的平面角的定义即可求出.
方法二:通过建立空间直角坐标系,利用平面的法向量所成的夹角来求两平面的二面角的平面角.
解答:解:(I)证明:过点Q作QD⊥BC于点D,
∵平面QBC⊥平面ABC,∴QD⊥平面ABC,
又∵PA⊥平面ABC,
∴QD∥PA,又∵QD?平面QBC,PA?平面QBC,
∴PA∥平面QBC.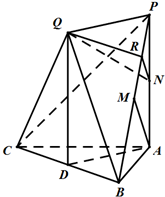
(Ⅱ)方法一:∵PQ⊥平面QBC,
∴∠PQB=∠PQC=90°,又∵PB=PC,PQ=PQ,
∴△PQB≌△PQC,∴BQ=CQ.
∴点D是BC的中点,连接AD,则AD⊥BC,
∴AD⊥平面QBC,∴PQ∥AD,AD⊥QD,
∴四边形PADQ是矩形.
设PA=2a,
∴PQ=AD=
a,PB=2
a,∴BQ=
a.
过Q作QR⊥PB于点R,
∴QR=
=
a,
PR=
=
=
a,
取PB中点M,连接AM,取PA的中点N,连接RN,
∵PR=
PB=
PM,PN=
PA,∴MA∥RN.
∵PA=AB,∴AM⊥PB,∴RN⊥PB.
∴∠QRN为二面角Q-PB-A的平面角.
连接QN,则QN=
=
=
a.又RN=
a,
∴cos∠QRN=
=
=-
.
即二面角Q-PB-A的余弦值为-
.
(Ⅱ)方法二:∵PQ⊥平面QBC,
∴∠PQB=∠PQC=90°,又∵PB=PC,PQ=PQ,
∴△PQB≌△PQC,∴BQ=CQ.
∴点D是BC的中点,连AD,则AD⊥BC.
∴AD⊥平面QBC,∴PQ∥AD,AD⊥QD,
∴四边形PADQ是矩形.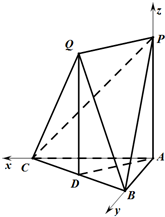
分别以AC、AB、AP为x、y、z轴建立空间直角坐标系O-xyz.
不妨设PA=2,则Q(1,1,2),B(0,2,0),P(0,0,2),
设平面QPB的法向量为
=(x,y,z).
∵
=(1,1,0),
=(0,2,-2).
∴
令x=1,则y=z=-1.
又∵平面PAB的法向量为
=(1,0,0).
设二面角Q-PB-A为θ,则|cosθ|=|cos<
,
>|=
=
又∵二面角Q-PB-A是钝角
∴cosθ=-
.
∵平面QBC⊥平面ABC,∴QD⊥平面ABC,
又∵PA⊥平面ABC,
∴QD∥PA,又∵QD?平面QBC,PA?平面QBC,
∴PA∥平面QBC.

(Ⅱ)方法一:∵PQ⊥平面QBC,
∴∠PQB=∠PQC=90°,又∵PB=PC,PQ=PQ,
∴△PQB≌△PQC,∴BQ=CQ.
∴点D是BC的中点,连接AD,则AD⊥BC,
∴AD⊥平面QBC,∴PQ∥AD,AD⊥QD,
∴四边形PADQ是矩形.
设PA=2a,
∴PQ=AD=
| 2 |
| 2 |
| 6 |
过Q作QR⊥PB于点R,
∴QR=
| ||||
2
|
| ||
| 2 |
PR=
| PQ2 |
| PB |
| 2a2 | ||
2
|
| ||
| 2 |
取PB中点M,连接AM,取PA的中点N,连接RN,
∵PR=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∵PA=AB,∴AM⊥PB,∴RN⊥PB.
∴∠QRN为二面角Q-PB-A的平面角.
连接QN,则QN=
| QP2+PN2 |
| 2a2+a2 |
| 3 |
| ||
| 2 |
∴cos∠QRN=
| QR2+RN2-QN2 |
| 2QR•RN |
| ||||||||
2×
|
| ||
| 3 |
即二面角Q-PB-A的余弦值为-
| ||
| 3 |
(Ⅱ)方法二:∵PQ⊥平面QBC,
∴∠PQB=∠PQC=90°,又∵PB=PC,PQ=PQ,
∴△PQB≌△PQC,∴BQ=CQ.
∴点D是BC的中点,连AD,则AD⊥BC.
∴AD⊥平面QBC,∴PQ∥AD,AD⊥QD,
∴四边形PADQ是矩形.

分别以AC、AB、AP为x、y、z轴建立空间直角坐标系O-xyz.
不妨设PA=2,则Q(1,1,2),B(0,2,0),P(0,0,2),
设平面QPB的法向量为
| n |
∵
| PQ |
| PB |
∴
|
又∵平面PAB的法向量为
| m |
设二面角Q-PB-A为θ,则|cosθ|=|cos<
| m |
| n |
|
| ||||
|
|
| ||
| 3 |
又∵二面角Q-PB-A是钝角
∴cosθ=-
| ||
| 3 |
点评:熟练掌握线面垂直的性质定理及线面平行的判定定理、二面角的定义及通过建立空间直角坐标系并利用平面的法向量所成的夹角来求二面角的平面角是解题的关键.

练习册系列答案
相关题目
 (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC,
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC,