题目内容
(2013•温州一模)方程(x-1)•sinπx=1在(-1,3)上有四个不同的根x1,x2,x3,x4,则x1+x2+x3+x4
4
4
.分析:方程(x-1)•sinπx=1即sinπx=
.根据函数f(x)=sinπx和g(x)=
的解析式,可以得到函数的图象关于点(1,0)对称,因此sinπx=
.的四个根分别为x1、x2、x3、x4两两关于点(1,0)对称,因此x1+x2+x3+x4=4.
| 1 |
| x-1 |
| 1 |
| x-1 |
| 1 |
| x-1 |
解答: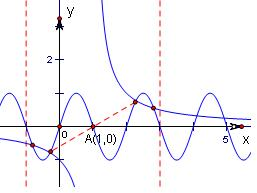 解:方程(x-1)•sinπx=1即sinπx=
解:方程(x-1)•sinπx=1即sinπx=
.
设函数f(x)=sinπx和g(x)=
.其图象如图所示.
则这两个函数的图象关于点(1,0)对称,
∵方程(x-1)•sinπx=1在(-1,3)上有四个不同的根x1,x2,x3,x4,
∴x1+x2+x3+x4=4,
故答案为:4.
 解:方程(x-1)•sinπx=1即sinπx=
解:方程(x-1)•sinπx=1即sinπx=| 1 |
| x-1 |
设函数f(x)=sinπx和g(x)=
| 1 |
| x-1 |
则这两个函数的图象关于点(1,0)对称,
∵方程(x-1)•sinπx=1在(-1,3)上有四个不同的根x1,x2,x3,x4,
∴x1+x2+x3+x4=4,
故答案为:4.
点评:本题考查根的存在性及根的个数判断,根据函数的解析式求得函数的对称性是解题的关键,属中档题.

练习册系列答案
相关题目
 (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC. (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC,
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC,