题目内容
 (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC,
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC,(Ⅰ)求证:PA∥平面QBC;
(Ⅱ)若PQ⊥平面QBC,求CQ与平面PBC所成角的正弦值.
分析:(I)过点Q作QD⊥BC于点D,利用面面垂直的性质定理可得QD⊥平面ABC.又PA⊥平面ABC,利用线面垂直的性质定理可得QD∥PA,再利用线面平行的判定定理即可证明;
(II)由已知可证明△PQB≌△PQC,得到BQ=CQ.根据点D是BC的中点,连接AD,则AD⊥BC.利用线面垂直的判定定理可得AD⊥平面QBC,于是PQ∥AD,AD⊥QD.得到四边形PADQ是矩形.设AB=AC=2a,则PQ=AD=
a,PD=
a.又BC⊥PA,BC⊥PQ,可得BC⊥平面PADQ,从而平面PBC⊥平面PADQ,过Q作QH⊥PD于点H,则QH⊥平面PBC.得到∠QCH是CQ与平面PBC所成的角.再利用边角关系即可得出.
(II)由已知可证明△PQB≌△PQC,得到BQ=CQ.根据点D是BC的中点,连接AD,则AD⊥BC.利用线面垂直的判定定理可得AD⊥平面QBC,于是PQ∥AD,AD⊥QD.得到四边形PADQ是矩形.设AB=AC=2a,则PQ=AD=
| 2 |
| 6 |
解答:(Ⅰ)证明:过点Q作QD⊥BC于点D,
∵平面QBC⊥平面ABC,∴QD⊥平面ABC.
又∵PA⊥平面ABC,
∴QD∥PA,
又∵QD?平面QBC,PA?平面QBC,
∴PA∥平面QBC.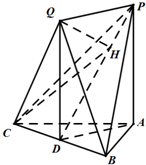
(Ⅱ)∵PQ⊥平面QBC,
∴∠PQB=∠PQC=90°,又∵PB=PC,PQ=PQ,
∴△PQB≌△PQC,∴BQ=CQ.
∴点D是BC的中点,连接AD,则AD⊥BC.
∴AD⊥平面QBC,∴PQ∥AD,AD⊥QD.
∴四边形PADQ是矩形.
设PA=AB=AC=2a,
则PQ=AD=
a,PD=
a.
又∵BC⊥PA,BC⊥PQ,∴BC⊥平面PADQ,
从而平面PBC⊥平面PADQ,过Q作QH⊥PD于点H,则QH⊥平面PBC.
∴∠QCH是CQ与平面PBC所成的角.
在Rt△PQD中,PQ•QD=PD•QH,则QH=
=
a,CQ=BQ=
a.
∴sin∠QCH=
=
×
=
.
∴CQ与平面PBC所成角的正弦值为
.
∵平面QBC⊥平面ABC,∴QD⊥平面ABC.
又∵PA⊥平面ABC,
∴QD∥PA,
又∵QD?平面QBC,PA?平面QBC,
∴PA∥平面QBC.

(Ⅱ)∵PQ⊥平面QBC,
∴∠PQB=∠PQC=90°,又∵PB=PC,PQ=PQ,
∴△PQB≌△PQC,∴BQ=CQ.
∴点D是BC的中点,连接AD,则AD⊥BC.
∴AD⊥平面QBC,∴PQ∥AD,AD⊥QD.
∴四边形PADQ是矩形.
设PA=AB=AC=2a,
则PQ=AD=
| 2 |
| 6 |
又∵BC⊥PA,BC⊥PQ,∴BC⊥平面PADQ,
从而平面PBC⊥平面PADQ,过Q作QH⊥PD于点H,则QH⊥平面PBC.
∴∠QCH是CQ与平面PBC所成的角.
在Rt△PQD中,PQ•QD=PD•QH,则QH=
2•
| ||
|
2
| ||
| 3 |
| 6 |
∴sin∠QCH=
| QH |
| CQ |
2
| ||
| 3 |
| 1 | ||
|
| ||
| 3 |
∴CQ与平面PBC所成角的正弦值为
| ||
| 3 |
点评:熟练掌握空间中的线面、面面垂直的判定与性质定理、线面角的定义、矩形的判定与性质定理、三角形全等的判定与性质定理、等积变形是解题的关键.

练习册系列答案
相关题目
 (2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.
(2013•温州一模)如图,已知平面QBC与直线PA均垂直于Rt△ABC所在平面,且PA=AB=AC.