Question

【题目】已知向量 =（2 cosx，cosx）， =（sinx，2cosx）（x∈R），设函数f（x）= ﹣1． （Ⅰ）求函数f（x）的单调减区间；
（Ⅱ）已知锐角△ABC的三个内角分别为A，B，C，若f（A）=2，B= ，边AB=3，求边BC．

Answer 1

【答案】解：（Ⅰ）f（x）= ﹣1=2 cosxsinx+2cos2x﹣1= sin2x+cos2x=2sin（2x+ ）， 令2kπ+ ≤2x+ ≤2kπ+ ，
可得函数f（x）的单调减区间[kπ+ ，kπ+ ]（k∈Z）；
（Ⅱ）f（A）=2sin（2A+ ）=2，∴A= ，
∵B= ，∴C= ，
∴sin = ，
∵AB=3，
∴BC= =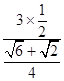
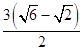
【解析】（Ⅰ）利用向量的数量积公式，结合二倍角、辅助角公式化简，再求函数f（x）的单调减区间；（Ⅱ）求出A= ，C= ，利用正弦定理，求出边BC．