Question

【题目】已知椭圆C： =1（a＞b＞0）的短轴长为2 ，离心率为 ，点F为其在y轴正半轴上的焦点． （Ⅰ）求椭圆C的方程；
（Ⅱ）若一动圆过点F，且与直线y=﹣1相切，求动圆圆心轨迹C1的方程；
（Ⅲ）过F作互相垂直的两条直线l1 ， l2 ， 其中l1交曲线C1于M、N两点，l2交椭圆C于P、Q两点，求四边形PMQN面积的最小值．

Answer 1

【答案】解：（I）由题意可得：2b=2 ， ，又a2=b2+c2 ， 联立解得b= ，a=2，c=1．
∴椭圆C的方程为 =1．
（II）F（0，1），由题意可得：动圆圆心轨迹为抛物线，点F为焦点，直线y=﹣1为准线，
因此C1的方程为：x2=4y．
（III）解：由题意可设直线l1的方程为：y=kx+1，（k≠0），M（x1 ， y1），N（x2 ， y2）．
则直线l1的方程为：y=﹣ x+1，P（x3 ， y3），Q（x4 ， y4）．
联立 ，可得：x2﹣4kx﹣4=0，可得x1+x2=4k，x1x2=﹣4，
∴|MN|= =4（1+k2）．
同理可得|PQ|=4 ，
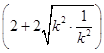∴S四边形PMQN= |MN||PQ|=8（1+k2） =8 ≥8 =32，
当且仅当k=±1时取等号，此时四边形PMQN面积的最小值为32
【解析】（I）由题意可得：2b=2 ， ，又a2=b2+c2 ， 联立解得即可得出．（II）F（0，1），由题意可得：动圆圆心轨迹为抛物线，点F为焦点，直线y=﹣1为准线，即可得出方程．（III）由题意可设直线l1的方程为：y=kx+1，（k≠0），M（x1 ， y1），N（x2 ， y2）． 则直线l1的方程为：y=﹣ x+1，P（x3 ， y3），Q（x4 ， y4）．与抛物线方程联立可得：x2﹣4kx﹣4=0，利用根与系数的关系代入|MN|= =4（1+k2）．同理可得|PQ|=4 ，利用S四边形PMQN= |MN||PQ|，及其基本不等式的性质即可得出．