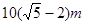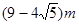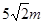题目内容
如图所示的七面体是由三棱台ABC – A1B1C1和四棱锥D- AA1C1C对接而成,四边形ABCD是边长为2的正方形,BB1⊥平面ABCD,BB1=2A1B1=2.
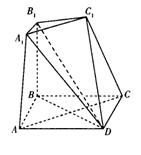
(I)求证:平面AA1C1C1⊥平面BB1D;
(Ⅱ)求二面角A –A1D—C1的余弦值.

(I)求证:平面AA1C1C1⊥平面BB1D;
(Ⅱ)求二面角A –A1D—C1的余弦值.
(Ⅰ)略(Ⅱ)余弦值为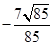
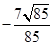
本试题主要是考查了空间几何体中面面垂直的关系的证明和二面角的求解的综合运用。
(1)建立合理的空间直角坐标系,然后要证明面面垂直,先证明两个平面的法向量是不是垂直即可。
(2)对于二面角的求解,结合图形的特点,表示出点的坐标,进而得到向量的坐标,求解平面的法向量,然后借助于向量的夹角公式得到二面角的平面角的大小
(1)建立合理的空间直角坐标系,然后要证明面面垂直,先证明两个平面的法向量是不是垂直即可。
(2)对于二面角的求解,结合图形的特点,表示出点的坐标,进而得到向量的坐标,求解平面的法向量,然后借助于向量的夹角公式得到二面角的平面角的大小

练习册系列答案
相关题目

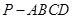 中,底面
中,底面 是矩形,
是矩形,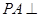 平面
平面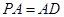 ,
,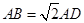 ,
,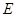 是线段
是线段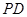 上的点,
上的点,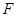 是线段
是线段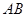 上的点,且
上的点,且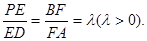

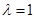 时,证明
时,证明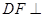 平面
平面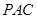 ;
;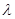 ,使异面直线
,使异面直线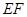 与
与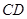 所成的角为
所成的角为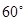 ?若存在,试求出
?若存在,试求出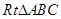 中,
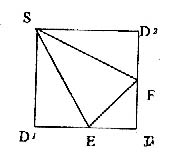
中,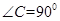 ,D,E分别为AC,AB的中点,点F为线段CD上的一点,将
,D,E分别为AC,AB的中点,点F为线段CD上的一点,将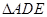 沿DE折起到
沿DE折起到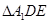 的位置,使
的位置,使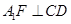 ,如图2.
,如图2.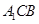
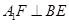
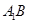 上是否存在点Q,使
上是否存在点Q,使 ?说明理由。
?说明理由。
 与平面
与平面 平行的是( )
平行的是( )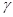
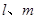 是
是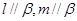
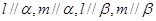
 、
、 ,平面
,平面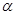 、
、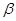 ,给出下列命题:
,给出下列命题: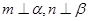 ,且
,且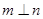 ,则
,则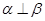 ②若
②若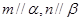 ,且
,且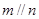 ,则
,则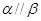
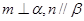 ,且
,且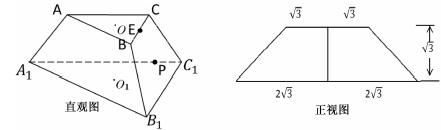
 处,同一时刻,一个长
处,同一时刻,一个长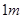 ,一端接触地面且与地面垂直的竹竿的影子长为
,一端接触地面且与地面垂直的竹竿的影子长为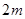 ,则该球的半径等于( )
,则该球的半径等于( )