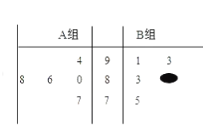
题目内容
【题目】在正项等比数列{an}中, ![]() ,a6+a7=3,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为 .
,a6+a7=3,则满足a1+a2+…+an>a1a2…an的最大正整数n的值为 .
【答案】12
【解析】解:设正项等比数列{an}首项为a1 , 公比为q,
由题意可得 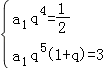 ,解之可得:a1=
,解之可得:a1= ![]() ,q=2,
,q=2,
故其通项公式为an= ![]() =2n﹣6 .
=2n﹣6 .
记Tn=a1+a2+…+an= ![]() =
= ![]() ,
,
Sn=a1a2…an=2﹣5×2﹣4…×2n﹣6=2﹣5﹣4+…+n﹣6= ![]() .
.
由题意可得Tn>Sn , 即 ![]() >
> ![]() ,
,
化简得:2n﹣1> ![]() ,即2n﹣
,即2n﹣ ![]() >1,
>1,
因此只须n> ![]() ,即n2﹣13n+10<0
,即n2﹣13n+10<0
解得 ![]() <n<
<n< ![]() ,
,
由于n为正整数,因此n最大为 ![]() 的整数部分,也就是12.
的整数部分,也就是12.
所以答案是:12
【考点精析】关于本题考查的解一元二次不等式和等差数列的前n项和公式,需要了解求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;前n项和公式:
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;前n项和公式:![]() 才能得出正确答案.
才能得出正确答案.

【题目】一个工厂在某年连续10个月每月产品的总成本y(万元)与该月产量x(万件)之间有如下一组数据:
x | 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
y | 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
(1)通过画散点图,发现可用线性回归模型拟合y与x的关系,请用相关系数加以说明;
(2)①建立月总成本y与月产量x之间的回归方程;
②通过建立的y关于x的回归方程,估计某月产量为1.98万件时,此时产品的总成本为多少万元?
(均精确到0.001)
附注:①参考数据:![]() ,
,
![]() ,
,
②参考公式:相关系数 ,
,
回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: .
.
【题目】已知变量![]() 之间的线性回归方程为
之间的线性回归方程为![]() ,且变量
,且变量![]() 之间的一组相关数据如表所示,则下列说法错误的是( )
之间的一组相关数据如表所示,则下列说法错误的是( )
x | 6 | 8 | 10 | 12 |
y | 6 | m | 3 | 2 |
A. 变量![]() 之间呈现负相关关系
之间呈现负相关关系
B. ![]() 的值等于5
的值等于5
C. 变量![]() 之间的相关系数
之间的相关系数![]()
D. 由表格数据知,该回归直线必过点(9,4)