题目内容
2.已知f(x)=a|x-2|,若f(f(x))<f(x)恒成立,则a的取值范围为a≤-1.分析 由f(f(x))<f(x)恒成立,可令x=2,解得a<0,再由若-1<a<0,则可取a=-$\frac{1}{2}$,可令x=6,检验不成立,再由a≤-1,作差比较,分析即可得到所求答案.
解答 解:f(f(x))<f(x)恒成立,即有f(f(2))<f(2),
即为f(0)<0,即有2a<0,即a<0,
若-1<a<0,则可取a=-$\frac{1}{2}$,即有f(x)=-$\frac{1}{2}$|x-2|,
当x=6时,f(6)=-2,f(f(6))=f(-2)=-2,
即有f(f(6))=f(6),故-1<a<0不成立;
若a≤-1,则f(x)=a|x-2|≤-|x-2|,
f(f(x))=f(a|x-2|)=a(2-a|x-2|)=2a-a2|x-2|,
由于a≤-1,则f(f(x))-f(x)=2a-(a2+a)|x-2|<0恒成立.
故答案为:a≤-1.
点评 本题考查了函数单调性与不等式的关系,以及绝对值函数的性质,注意运用特殊值法,考查推理判断能力.属于难题.

练习册系列答案
相关题目
7.从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如下: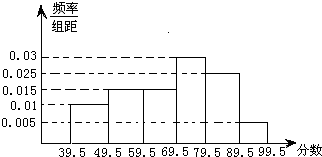
估计这次环保知识竞赛的及格率(60分及以上为及格)是( )

估计这次环保知识竞赛的及格率(60分及以上为及格)是( )
| A. | 7.5% | B. | 70% | C. | 2.5% | D. | 75% |
12.$\frac{(sin\frac{π}{10}+cos\frac{π}{10})(sin\frac{3π}{20}+cos\frac{3π}{20})}{cos\frac{π}{10}cos\frac{3π}{20}}$的值等于( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 1+$\sqrt{2}$ | D. | 2+$\sqrt{2}$ |