题目内容
【题目】已知函数![]() ,x∈R.
,x∈R.
(1)判断函数的奇偶性,并说明理由;
(2)利用函数单调性定义证明:![]() 在
在![]() 上是增函数;
上是增函数;
(3)若![]() 对任意的x∈R,任意的
对任意的x∈R,任意的![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
【答案】(1)![]() 是偶函数,证明详见解析;(2)详见解析;(3)
是偶函数,证明详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)由奇偶性定义判断证明;
(2)由单调性定义证明;
(3)设![]() ,换元后求出
,换元后求出![]() 的最大值
的最大值![]() ,由(2)求出
,由(2)求出![]() 有最小值
有最小值![]() ,然后解不等式
,然后解不等式![]() 可得k的范围.
可得k的范围.
(1)![]() 是偶函数.证明如下:
是偶函数.证明如下:
函数![]() 的定义域为
的定义域为![]() ,关于原点对称,
,关于原点对称,
∵![]() ,
,
∴ ![]() 是偶函数.
是偶函数.
(2)设![]() ,则
,则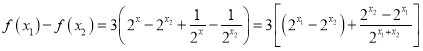
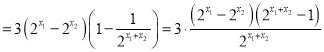 ,
,
由![]() ,知
,知![]() ,
,![]() ,于是
,于是![]() ,
,
∴![]() ,
,
∴ ![]() ,即
,即![]() ,
,
∴ ![]() 在
在![]() 上是增函数.
上是增函数.
(3![]() ,则
,则
![]()
![]()
![]() ,
,
令![]() ,易知
,易知![]() ,则
,则![]() ,
,
又∵ ![]() 是R上的偶函数,且在
是R上的偶函数,且在![]() 上单调递增,则该函数在区间
上单调递增,则该函数在区间![]() 上单调递减,∴
上单调递减,∴ ![]() ,
,
∴ 由题意只需4+k≤6,解得k≤2,即k的取值范围为![]() .
.

 巧学巧练系列答案
巧学巧练系列答案【题目】缴纳个人所得税是收入达到缴纳标准的公民应尽的义务.
①个人所得税率是个人所得税额与应纳税收入额之间的比例;
②应纳税收入额=月度收入-起征点金额-专项扣除金额(三险一金等);
③2018年8月31日,第十三届全国人民代表大会常务委员会第五次会议《关于修改中华人民共和国个人所得税法的决定》,将个税免征额(起征点金额)由3500元提高到5000元.下面两张表格分别是2012年和2018年的个人所得税税率表:
2012年1月1日实行:
级数 | 应纳税收入额(含税) | 税率( | 速算扣除数 |
一 | 不超过1500元的部分 | 3 | 0 |
二 | 超过1500元至4500元的部分 | 10 | 105 |
三 | 超过4500元至9000元的部分 | 20 | 555 |
四 | 超过9000元至35000元的部分 | 25 | 1005 |
五 | 超过35000元至55000元的部分 | 30 | 2755 |
六 | 超过55000元至80000元的部分 | 35 | 5505 |
七 | 超过80000元的部分 | 45 | 13505 |
2018年10月1日试行:
级数 | 应纳税收入额(含税) | 税率( | 速算扣除数 |
一 | 不超过3000元的部分 | 3 | 0 |
二 | 超过3000元至12000元的部分 | 10 | 210 |
三 | 超过12000元至25000元的部分 | 20 | 1410 |
四 | 超过25000元至35000元的部分 | 25 | 2660 |
五 | 超过35000元至55000元的部分 | 30 | 4410 |
六 | 超过55000元至80000元的部分 | 35 | 7160 |
七 | 超过80000元的部分 | 45 | 15160 |
(1)何老师每月工资收入均为13404元,专项扣除金额3710元,请问何老师10月份应缴纳多少元个人所得税?若与9月份相比,何老师增加收入多少元?
(2)对于财务人员来说,他们计算个人所得税的方法如下:应纳个人所得税税额=应纳税收入额×适用税率-速算扣除数,请解释这种计算方法的依据?

