题目内容
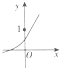
4.已知函数f(x)=1-a|x|(a>0,a≠1)的图象如图所示,则函数g(x)=$\frac{lo{g}_{a}|x|}{x}$的图象为( )
| A. |  | B. |  | C. |  | D. |  |
分析 分析函数的奇偶性,零点,及函数图象所在象限,利用排除法排除错误答案,可得正解.
解答 解:∵函数g(x)=$\frac{lo{g}_{a}|x|}{x}$为奇函数,
故函数图象应关于原点对称,故排除D答案;
又由g(1)=0,可知,函数图象过(1,0)点,故排除答案C;
由已知中函数f(x)=1-a|x|(a>0,a≠1)的图象,可得:a>1,
故x>1时,g(x)>0,即此时函数图象应在第一象限,故排除A,
故选:B
点评 本题考查的知识点是函数的图象,其中正确理解函数的奇偶性,特殊点等性质是解答的关键.

练习册系列答案
相关题目
14.设反比例函数f(x)=$\frac{1}{x}$与二次函数g(x)=ax2+bx的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),且x1<x2,则$\frac{y_1}{y_2}$=( )
| A. | 2或$\frac{1}{2}$ | B. | -2或$-\frac{1}{2}$ | C. | 2或$-\frac{1}{2}$ | D. | -2或$\frac{1}{2}$ |

 如图,过抛物线y2=2px(p>0)焦点F的直线交抛物线于A,B两点,O为坐标原点,C为抛物线准线与x轴的交点,且∠CFA=135°,则tan∠ACB=2$\sqrt{2}$.
如图,过抛物线y2=2px(p>0)焦点F的直线交抛物线于A,B两点,O为坐标原点,C为抛物线准线与x轴的交点,且∠CFA=135°,则tan∠ACB=2$\sqrt{2}$. 已知函数f(x)=loga(2x+b-l)(a>0,a≠1的图象如图所示,则函数g(x)=ax-b的图象为( )
已知函数f(x)=loga(2x+b-l)(a>0,a≠1的图象如图所示,则函数g(x)=ax-b的图象为( )