题目内容
13.若曲线y=e-x上点P处的切线平行于直线2x+y+1=0,则点P的坐标为(-ln2,2).分析 先设P(x,y),对函数求导,由在在点P处的切线与直线2x+y+1=0平行,求出x,最后求出y.
解答 解:设P(x,y),则y=e-x,
∵y′=-e-x,在点P处的切线与直线2x+y+1=0平行,
令-e-x=-2,解得x=-ln2,
∴y=e-x=2,故P(-ln2,2).
故答案为:(-ln2,2).
点评 本题考查了导数的几何意义,即点P处的切线的斜率是该点出的导数值,以及切点在曲线上和切线上的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.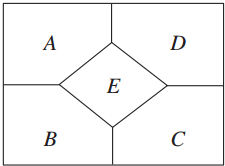 如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
 如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )
如图所示的五个区域中,现有四种颜色可供选择.要求每一个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为( )| A. | 24种 | B. | 48种 | C. | 72种 | D. | 96种 |
 如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,CA=CB=2,若$\overrightarrow{AB}$•$\overrightarrow{AE}$+
如图,在△ABC和△AEF中,B是EF的中点,AB=EF=1,CA=CB=2,若$\overrightarrow{AB}$•$\overrightarrow{AE}$+ 如图,已知△OCB中,B、C关于点A对称,D是将OB分成2:1的一个内分点,DC和OA交于点E,设$\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b$.
如图,已知△OCB中,B、C关于点A对称,D是将OB分成2:1的一个内分点,DC和OA交于点E,设$\overrightarrow{OA}=\overrightarrow a,\overrightarrow{OB}=\overrightarrow b$.