题目内容
已知数列{an}满足a1=3,an+1=an+p·3n(n∈N*,p为常数),a1,a2+6,a3成等差数列.
(1)求p的值及数列{an}的通项公式;
(2)设数列{bn}满足bn=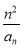 ,证明:bn≤
,证明:bn≤ .
.
(1)an=3n(2)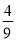
【解析】由a1=3,an+1=an+p·3n,得a2=3+3p,a3=a2+9p=3+12p.
∵a1,a2+6,a3成等差数列,∴a1+a3=2(a2+6),即3+3+12p=2(3+3p+6),得p=2.
依题意知,an+1=an+2×3n,
当n≥2时,a2-a1=2×31,a3-a2=2×32,…,an-an-1=2×3n-1.
等号两边分别相加得an-a1=2(31+32+…+3n-1)=2×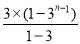 =3n-3,
=3n-3,
∴an-a1=3n-3,∴an=3n(n≥2).
又a1=3适合上式,故an=3n.
(2)证明:∵an=3n,∴bn=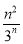 .
.
∵bn+1-bn=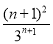 -
-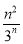 =
=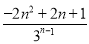 (n∈N*).
(n∈N*).
若-2n2+2n+1<0,则n> ,
,
即当n≥2时,有bn+1<bn.
又因为b1=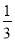 ,b2<
,b2<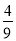 .故bn≤
.故bn≤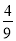

练习册系列答案
相关题目