题目内容
1.一元二次不等式(x-2)(x-3)<0的解集为{x|2<x<3}.分析 根据一元二次不等式与对应方程解的关系,写出不等式的解集即可.
解答 解:一元二次不等式(x-2)(x-3)<0,
对应的方程为(x-2)(x-3)=0,
解方程,得x=2,或x=3,
所以,不等式(x-2)(x-3)<0的解集为
{x|2<x<3}.
故答案为:{x|2<x<3}.
点评 本题考查了求一元二次不等式的解集的应用问题,是基础题目.

练习册系列答案
相关题目
12.三角形ABC满足,|$\overrightarrow{AB}+\overrightarrow{AC}$|=|$\overrightarrow{AB}-\overrightarrow{AC}$|,点M为边BC的中点,且|$\overrightarrow{AM}$|=4,$\overrightarrow{AM}•(\overrightarrow{AB}-\overrightarrow{AC})$=0,则边AC的长度为( )
| A. | 4$\sqrt{2}$ | B. | 4 | C. | 8$\sqrt{2}$ | D. | 8 |
13.已知a∈R,若f(x)=$\frac{1}{2}{x^2}$-|x-2a|有三个或四个零点,则g(x)=ax2+4x+1的零点个数为( )
| A. | 2 | B. | 1或2 | C. | 0或2 | D. | 0或1 |
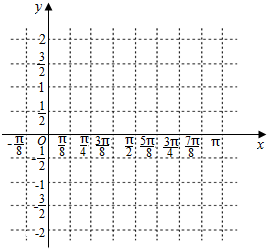 已知函数f(x)=2cosx(sinx-cosx)+1.
已知函数f(x)=2cosx(sinx-cosx)+1.