题目内容
【题目】设Sn是等差数列{an}的前n项和,已知![]() 与
与![]() 的等比中项为
的等比中项为![]() ,且
,且![]() 与
与![]() 的等差中项为1,求数列{an}的通项公式。
的等差中项为1,求数列{an}的通项公式。
【答案】![]() 或
或![]() .
.
【解析】
设等差数列{an}的首项为a1,公差为d,运用等差中项和等比中项的定义,利用等差数列的求和公式,代入可求a1,d,解方程可求通项an.
设等差数列{an}的首项![]() ,公差为
,公差为![]() ,则通项为
,则通项为![]() ,
,
前![]() 项和为
项和为![]() ,依题意有
,依题意有 ,
,
其中![]() ,由此可得
,由此可得 ,
,
整理得 , 解方程组得
, 解方程组得![]() 或
或 ,
,
由此得![]() ;或
;或![]() .
.
经检验![]() 和
和![]() 均合题意.
均合题意.
所以所求等差数列的通项公式为![]() 或
或![]() .
.
【点睛】
本题主要考查了等差数列的通项公式和性质及等比数列中项的性质,数列通项的求法中有常见的已知![]() 和
和![]() 的关系,求
的关系,求![]() 表达式,一般是写出
表达式,一般是写出![]() 做差得通项,但是这种方法需要检验n=1时通项公式是否适用。
做差得通项,但是这种方法需要检验n=1时通项公式是否适用。
【题型】解答题
【结束】
20
【题目】等差数列{an}的各项均为正数,a1=3,前n项和为Sn,{bn}为等比数列,b1=1,且b2S2=64,b3S3=960.
(1)求an与bn;
(2)求![]()
【答案】(1)an=2n+1,bn=8n-1.(2)![]()
【解析】
(1)设{an}的公差为d,{bn}的公比为q,由题设条件建立方程组,解方程组得到d和q的值,从而求出an与bn;(2)由Sn=n(n+2),知![]() ,由此可求出
,由此可求出![]() 的值.
的值.
(1)设{an}的公差为d,{bn}的公比为q,则d为正数,
an=3+(n-1)d,bn=qn-1,
依题意有![]() ,
,
解得![]() 或
或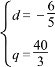 (舍去).
(舍去).
故an=3+2(n-1)=2n+1,bn=8n-1.
(2)Sn=3+5+…+(2n+1)=n(n+2).
所以![]() +
+![]() +…+
+…+![]() =
=![]() +
+![]() +
+![]() +…+
+…+![]()
=![]() (1-
(1-![]() +
+![]() -
-![]() +
+![]() -
-![]() +…+
+…+![]() -
-![]() )
)
=![]() (1+
(1+![]() -
-![]() -
-![]() )
)
=![]() -
-![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
