题目内容
【题目】已知直线x﹣2y+2与圆C:x2+y2﹣4y+m=0相交,截得的弦长为 ![]()
(1)求圆C的方程;
(2)过点M(﹣1,0)作圆C的切线,求切线的直线方程;
(3)若抛物线y=x2上任意三个不同的点P、Q、R,且满足直线PQ和PR都与圆C相切,判断直线QR与圆C的位置关系,并加以证明.
【答案】
(1)解:圆心C(0,2)到直线x﹣2y+2与的距离为d= ![]() ,
,
∵截得的弦长为 ![]() ,∴r=1
,∴r=1
∴圆C的方程为:x2+(y﹣2)2=1
(2)解:斜率不存在时,x=﹣1满足题意;
斜率存在时,设直线方程为y=k(x+1),即kx﹣y+k=0,
圆心到直线的距离d= ![]() =1,∴k=﹣
=1,∴k=﹣ ![]() ,切线方程为3x+4y+3=0,
,切线方程为3x+4y+3=0,
综上所述,切线方程为x=﹣1或3x+4y+3=0
(3)解:设P(a,a2),Q(b,b2),R(c,c2),可得kPQ=a+b,
直线PQ的方程为y﹣a2=(a+b)(x﹣a),即为y=(a+b)x﹣ab,
同理可得,直线PR的方程为y=(a+c)x﹣ac,
直线QR的方程为y=(b+c)x﹣bc,
∵直线PQ和PR都与圆C相切,
∴ 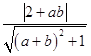 =1,
=1, 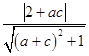 =1,即为b2(1﹣a2)﹣2ab+a2﹣3=0,
=1,即为b2(1﹣a2)﹣2ab+a2﹣3=0,
c2(1﹣a2)﹣2ac+a2﹣3=0,即有b,c为方程x2(1﹣a2)﹣2ax+a2﹣3=0的两根,
可得b+c= ![]() ,bc=
,bc= ![]() ,
,
由圆心到直线QR的距离为 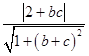 =1,
=1,
则直线QR与圆C相切
【解析】(1)求得圆心到直线的距离,由弦长公式,计算即可得到m=3,进而得到圆的方程;(2)分类讨论,运用直线和圆相切的条件,求得k,即可得出结论;(3)设P(a,a2),Q(b,b2),R(c,c2),求得直线PQ,PR,QR的方程,运用直线和圆相切的条件,化简整理,再由韦达定理,可得b,c的关系,再由圆心到直线QR的距离,即可判断所求位置关系.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案






