题目内容
【题目】已知等差数列{an}的前n项和为Sn ， 且S3=9，a2a4=21，数列{bn}满足 
，若 
，则n的最小值为（ ）
A.6
B.7
C.8
D.9
【答案】C
【解析】解：设等差数列{an}的公差为d，∵S3=9，a2a4=21，∴3a1+ 
d=9，（a1+d）（a1+3d）=21，
联立解得：a1=1，d=2．
∴an=1+2（n﹣1）=2n﹣1．
∵数列{bn}满足 
，
∴n=1时， 
=1﹣ 
，解得b1= ．
n≥2时， 
+…+ 
=1﹣ 
，
∴ 
= 
．
∴bn= 
．
若 
，则 ＜ 
．
n=7时， 
＞ ．
n=8时， 
＜ ．
因此： ，则n的最小值为8．
故选：C．
【考点精析】认真审题，首先需要了解等差数列的通项公式（及其变式）(通项公式：
或
)．
阅读快车系列答案
【题目】为推行“新课堂”教学法，某化学老师分别用传统教学和“新课堂”两种不同的教学方式，在甲、乙两个平行班级进行教学实验，为了比较教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，结果如下表：记成绩不低于70分者为“成绩优良”．
分数 | [50,59) | [60,69) | [70,79) | [80,89) | [90,100] |
甲班频数 | 5 | 6 | 4 | 4 | 1 |
乙班频数 | 1 | 3 | 6 | 5 | 5 |
（1）由以上统计数据填写下面2×2列联表，并判断“成绩优良与教学方式是否有关”?
甲班 | 乙班 | 总计 | |
成绩优良 | |||
成绩不优良 | |||
总计 |
现从上述40人中，学校按成绩是否优良采用分层抽样的方法抽取8人进行考核．在这8人中，记成绩不优良的乙班人数为
，求的分布列及数学期望．
附：
． 临界值表
【题目】随着生活水平的提高，越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣，下图为其等高条形图：
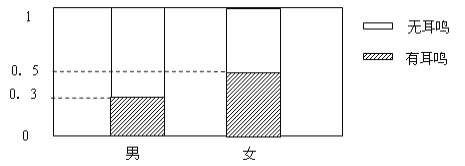
绘出2×2列联表；
②根据列联表的独立性检验，能否在犯错误的概率不超过0.05的前提下认为耳鸣与性别有关系？
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
附：
