题目内容
【题目】已知函数f(x)= ![]() ,(ω>0),其最小正周期为
,(ω>0),其最小正周期为 ![]() .
.
(1)求f(x)的表达式;
(2)将函数f(x)的图象向右平移 ![]() 个单位,再将图象上各点的横坐标伸长到原来的4倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+m=0在区间
个单位,再将图象上各点的横坐标伸长到原来的4倍(纵坐标不变),得到函数y=g(x)的图象,若关于x的方程g(x)+m=0在区间 ![]() 上有且只有一个实数解,求实数m的取值范围.
上有且只有一个实数解,求实数m的取值范围.
【答案】
(1)解: ![]()
= ![]() ,
,
由题意知f(x)的最小正周期 ![]() ,
, ![]() ,
,
所以ω=2,
所以 ![]() .
.
(2)解:将f(x)的图象向右平移 ![]() 个单位后,得到y=sin4x的图象;
个单位后,得到y=sin4x的图象;
再将所得图象所有点的横坐标伸长到原来的4倍(纵坐标不变),得到y=sinx的图象,
所以g(x)=sinx,g(x)+m=0在区间 ![]() 上有且只有一个实数解,即函数y=g(x)与y=﹣m在区间
上有且只有一个实数解,即函数y=g(x)与y=﹣m在区间 ![]() 上有且只有一个交点,
上有且只有一个交点,
由正弦函数的图象可知 ![]() ,
,
解得 ![]() ,
,
所以实数m的取值范围是 ![]() .
.
【解析】(1)利用三角函数恒等变换的应用化简函数解析式可得f(x)= ![]() ,由题意及周期公式可求ω的值,即可得解.(2)由函数y=Asin(ωx+φ)的图象变换规律可得g(x)=sinx,在区间
,由题意及周期公式可求ω的值,即可得解.(2)由函数y=Asin(ωx+φ)的图象变换规律可得g(x)=sinx,在区间 ![]() 上有且只有一个实数解,即函数y=g(x)与y=﹣m在区间
上有且只有一个实数解,即函数y=g(x)与y=﹣m在区间 ![]() 上有且只有一个交点,由正弦函数的图象可解得实数m的取值范围.
上有且只有一个交点,由正弦函数的图象可解得实数m的取值范围.
【考点精析】根据题目的已知条件,利用函数y=Asin(ωx+φ)的图象变换的相关知识可以得到问题的答案,需要掌握图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象.
的图象.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案【题目】已知某校5个学生的数学和物理成绩如表
学生的编号i | 1 | 2 | 3 | 4 | 5 |
数学xi | 80 | 75 | 70 | 65 | 60 |
物理yi | 70 | 66 | 68 | 64 | 62 |
(Ⅰ)假设在对这5名学生成绩进行统计时,把这5名学生的物理成绩搞乱了,数学成绩没出现问题,问:恰有2名学生的物理成绩是自己的实际分数的概率是多少?
(Ⅱ)通过大量事实证明发现,一个学生的数学成绩和物理成绩具有很强的线性相关关系的,在上述表格是正确的前提下,用x表示数学成绩,用y表示物理成绩,求y与x的回归方程;
参考公式: ![]() =
= 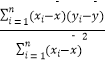 ,
, ![]() .
.