题目内容
(本小题满分14分)
已知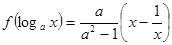
(Ⅰ)求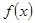 ;
;
(Ⅱ)判断并证明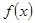 的奇偶性与单调性;
的奇偶性与单调性;
(Ⅲ)若对任意的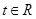 ,不等式
,不等式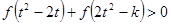 恒成立,求
恒成立,求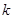 的取值范围。
的取值范围。
已知
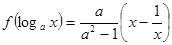
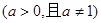
(Ⅰ)求
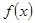 ;
;(Ⅱ)判断并证明
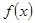 的奇偶性与单调性;
的奇偶性与单调性;(Ⅲ)若对任意的
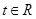 ,不等式
,不等式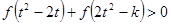 恒成立,求
恒成立,求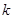 的取值范围。
的取值范围。(1)则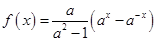
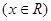 ;(2)函数
;(2)函数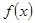 为奇函数。证明见解析。
为奇函数。证明见解析。
(3) .
.
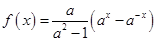
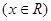 ;(2)函数
;(2)函数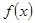 为奇函数。证明见解析。
为奇函数。证明见解析。(3)
 .
. 试题分析:(1)利用换元法:令t=logax⇒x=at,代入可得f(t)从而可得函数f(x)的解析式
(2)由(1)得f(x)定义域为R,可求函数的定义域,先证奇偶性:代入f(-x)=-f(x),从而可得函数为奇函数。再证单调性:利用定义任取x1<x2,利用作差比较f(x1)-f(x2)的正负,从而确当f(x1)与f(x2)的大小,进而判断函数的单调性
(3)根据上面的单调性的证明以及定义域得到不等式的求解。
解:(1)令
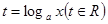
则
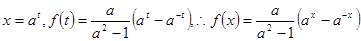
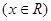 ………3分
………3分(2)
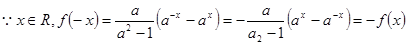
∴函数
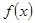 为奇函数。 ………5分
为奇函数。 ………5分当
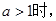 ,任取
,任取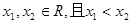
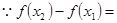
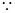
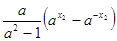 -
-
=
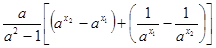 =
=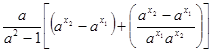
=
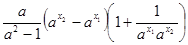
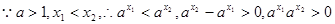 ,
,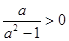
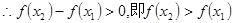
类似可证明当
 ,综上,无论
,综上,无论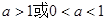 ,
,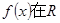 上都是增函数。 ………9分
上都是增函数。 ………9分(3)不等式化为
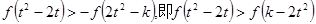
∵
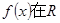 上都是增函数,∴
上都是增函数,∴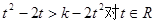 恒成立
恒成立即
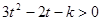
 对
对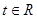 恒成立,∴
恒成立,∴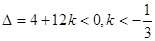
故
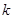 的取值范围
的取值范围 . ………14分
. ………14分点评:解题的关键是利用奇偶性的定义③利用定义判断函数单调性的步骤(i)任设x1<x2(也可x1>x2)(ii)作差f(x1)-f(x2)(iii)定号,给出结论.

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
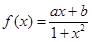 是定义在
是定义在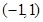 上的奇函数,且
上的奇函数,且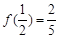 。
。 的解析式;
的解析式; 。
。 },B={y|1
},B={y|1 },下列图形表示集合A到集合B的函数图形的是( )
},下列图形表示集合A到集合B的函数图形的是( )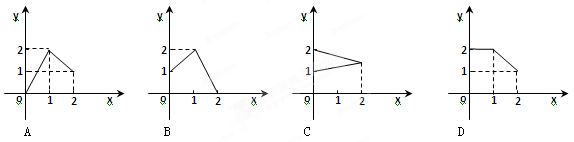
 ,若同时满足下列条件:①
,若同时满足下列条件:① 在D内单调递增或单调递减;②存在区间[
在D内单调递增或单调递减;②存在区间[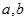 ]
]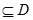 ,使
,使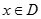 )叫闭函数.
)叫闭函数.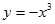 符合条件②的区间[
符合条件②的区间[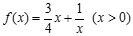 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;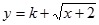 是闭函数,求实数
是闭函数,求实数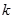 的取值范围.
的取值范围. ,
,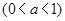
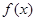 的定义域;
的定义域;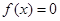 ,求
,求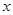 的值;
的值;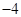 ,求
,求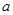 的值.
的值.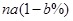
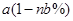
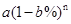
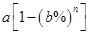
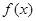 是定义在
是定义在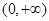 上的增函数,且对一切
上的增函数,且对一切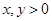 ,满足
,满足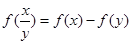 .
.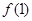 的值;
的值;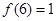 ,解不等式
,解不等式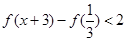
 上市销售40天内全部售完,该公司对第一批产品
上市销售40天内全部售完,该公司对第一批产品
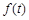 与第一批产品A上市时间t的关系式;
与第一批产品A上市时间t的关系式;