题目内容
下列命题:
①若直线上l有无数个点不在平面α内,l则//α;
②若直线l与平面α平行,则与平面内的任意一条直线都平行;
③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行;
④若直线l与平面α平行,则与平面内的任意一条直线都没有公共点.
其中正确的命题的序号是________(注:把你认为正确的命题的序号都填上)
①若直线上l有无数个点不在平面α内,l则//α;
②若直线l与平面α平行,则与平面内的任意一条直线都平行;
③如果两条平行直线中的一条直线与一个平面平行,那么另一条直线也与这个平面平行;
④若直线l与平面α平行,则与平面内的任意一条直线都没有公共点.
其中正确的命题的序号是________(注:把你认为正确的命题的序号都填上)
④
根据直线与平面之间的位置关系:依次分析命题,
①若直线与平面相交,则除了交点以外的任何一个点都不在平面内,这样的点有无数个;
②若直线l平行平面α,则l与平面α内的任意一条直线都没有公共点,所以l与平面α内的任一条直线有两种位置关系:平行、异面;
③此题需注意考虑直线是否有可能在平面内;
④若直线l与平面α平行,则l与平面α没有公共点,所以l与平面α内的任意一条直线都没有公共点.
解:①若直线与平面相交,则除了交点以外的无数个点都不在平面内,故①错误;
②若直线l平行平面α,则l与平面α内的任一条直线有两种位置关系:平行、异面,故②错误;
③如果两条平行直线中的一条与一个平面平行,那么另一条与这个平面可能平行,也有可能就在面内,故③错误;
④用反证法易得:若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点,故④正确.
故答案为④.
①若直线与平面相交,则除了交点以外的任何一个点都不在平面内,这样的点有无数个;
②若直线l平行平面α,则l与平面α内的任意一条直线都没有公共点,所以l与平面α内的任一条直线有两种位置关系:平行、异面;
③此题需注意考虑直线是否有可能在平面内;
④若直线l与平面α平行,则l与平面α没有公共点,所以l与平面α内的任意一条直线都没有公共点.
解:①若直线与平面相交,则除了交点以外的无数个点都不在平面内,故①错误;
②若直线l平行平面α,则l与平面α内的任一条直线有两种位置关系:平行、异面,故②错误;
③如果两条平行直线中的一条与一个平面平行,那么另一条与这个平面可能平行,也有可能就在面内,故③错误;
④用反证法易得:若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点,故④正确.
故答案为④.

练习册系列答案
相关题目
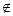 R ④{0}∈N
R ④{0}∈N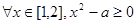 ”,命题q:“
”,命题q:“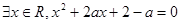 ”,
”,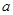 的取值范围是
的取值范围是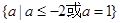 B.
B. 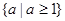
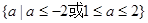 D.
D. 
 、
、 ,平面
,平面 、
、 ,给出下列命题:
,给出下列命题: ,且
,且 ,则
,则 ②若
②若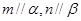 ,且
,且 ,则
,则
 ,且
,且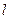
 和平面
和平面 ,下列命题中,真命题是
,下列命题中,真命题是 ,则
,则
 则
则
 ,则
,则 ,则
,则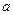 ∥直线
∥直线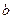 ”的必要不充分条件是“
”的必要不充分条件是“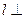 平面
平面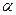 ”的充要条件是“
”的充要条件是“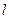 垂直于平面
垂直于平面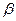 ”是“
”是“ ,若p和q有且仅有一个成立,则实数c的取值范围是
,若p和q有且仅有一个成立,则实数c的取值范围是