题目内容
9. 如图,已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{3}$,A1、A2分别为其左右顶点,过坐标原点且斜率为k(k≠0)的直线交双曲线C于P1、P2,则A1P1、A1P2、A2P1、A2P2这四条直线的斜率乘积为( )
如图,已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的离心率为$\sqrt{3}$,A1、A2分别为其左右顶点,过坐标原点且斜率为k(k≠0)的直线交双曲线C于P1、P2,则A1P1、A1P2、A2P1、A2P2这四条直线的斜率乘积为( )| A. | 8 | B. | 2 | C. | 6 | D. | 4 |
分析 设点,利用斜率公式,结合离心率为$\sqrt{3}$,即可得出结论.
解答 解:设P1(x,y),P2(m,n),则
A1P1、A1P2、A2P1、A2P2这四条直线的斜率乘积为$\frac{y}{x+a}•\frac{n}{m+a}•\frac{y}{x-a}•\frac{n}{m-a}$=$\frac{{y}^{2}}{{x}^{2}-{a}^{2}}•\frac{{n}^{2}}{{m}^{2}-{a}^{2}}$
=$\frac{{b}^{2}}{{a}^{2}}$$•\frac{{b}^{2}}{{a}^{2}}$,
∵离心率为$\sqrt{3}$,
∴$\frac{c}{a}$=$\sqrt{3}$,
∴$\frac{{b}^{2}}{{a}^{2}}$=2,
∴$\frac{{b}^{2}}{{a}^{2}}$$•\frac{{b}^{2}}{{a}^{2}}$=4,
∴A1P1、A1P2、A2P1、A2P2这四条直线的斜率乘积为4,
故选:D.
点评 本题考查双曲线的方程与性质,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
4.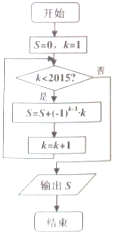 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )
 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )| A. | -1008 | B. | -1007 | C. | 1007 | D. | 1008 |