题目内容
定义在R上的函数f(x)满足f(x+2)=-f(x),且当x∈[-1,1]时,f(x)=x3.
(1)求f(x)在[1,5]上的表达式;
(2)若A={x| f(x)>a,x∈R},且A![]() ,求实数a的取值范围.
,求实数a的取值范围.
解:(1)(x+2)=--f(x), x∈R,∴f(x)= -f(x-2).
当x∈[1,3]时,x-2∈[-1,1],∴f(x)= -f(x-2)= -(x-2)3=(2-x)3.
又f(x)= -f(x+2)=f(x+4), ∴f(x)是以4为周期的函数.
当x∈[3,5]时,x-4∈[-1,1], f(x)=f(x-4)= (x-4)3.
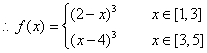
(2)当![]() 当x∈[3,5]时,y= f(x)=(x-4)3, ∴y∈[-1,1], ∴f(x)在[1,5]上的值域为[-1,1] ,又f(x)是以4为周期的函数,∴当x∈R时,f(x) ∈[-1,1]
当x∈[3,5]时,y= f(x)=(x-4)3, ∴y∈[-1,1], ∴f(x)在[1,5]上的值域为[-1,1] ,又f(x)是以4为周期的函数,∴当x∈R时,f(x) ∈[-1,1]
∴当a<1时,存在x使f(x)>a,故a的取值范围为a<1.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目