题目内容
已知函数f(x)=cos2x-sin2x+sin2x
(1)求f(x)的最大值和最小正周期;
(2)设α,β∈[0, ],f(
],f( +
+ )=
)= ,f(
,f(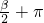 )=
)= ,求sin(α+β)的值.
,求sin(α+β)的值.
解:(1)∵f(x)=cos2x-sin2x+sin2x=cos2x+sin2x
= (
( cos2x+
cos2x+ sin2x)=
sin2x)= sin(2x+
sin(2x+ )…(3分)
)…(3分)
由振幅的意义可得,函数f(x)的最大值为 …(4分)
…(4分)
最小正周期T= =π…(5分)
=π…(5分)
(2)∵f( +
+ )=
)= sin(2(
sin(2( )+
)+ )=
)= sin(
sin(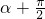 )=
)= cosα=
cosα= ,
,
∴cosα=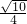 ,又因为α∈[0,
,又因为α∈[0, ],∴sinα=
],∴sinα= …(8分)
…(8分)
同理可得f( +π)=
+π)= sin(2(
sin(2(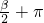 )+
)+ )=
)= sin(
sin(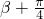 )=
)= ,…(9分)
,…(9分)
又因为β∈[0, ],∴
],∴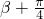 ∈[
∈[ ,
, ],∴
],∴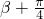 =
= ,解得β=
,解得β= …(11分)
…(11分)
∴sin(α+β)=sin( )=sinαcos
)=sinαcos +cosαsin
+cosαsin =
=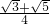 …(12分)
…(12分)
分析:(1)由三角函数的运算可得f(x)= sin(2x+
sin(2x+ ),易得最值和周期;
),易得最值和周期;
(2)由题意可得cosα=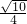 ,进而可得sinα=
,进而可得sinα= ,同理可得β=
,同理可得β= ,进而可得sin(α+β)=sin(
,进而可得sin(α+β)=sin( ),代入数值计算即可.
),代入数值计算即可.
点评:本题考查三角函数的化简和求值,涉及函数的周期和最值的求解,属中档题.
=
 (
( cos2x+
cos2x+ sin2x)=
sin2x)= sin(2x+
sin(2x+ )…(3分)
)…(3分)由振幅的意义可得,函数f(x)的最大值为
 …(4分)
…(4分)最小正周期T=
 =π…(5分)
=π…(5分)(2)∵f(
 +
+ )=
)= sin(2(
sin(2( )+
)+ )=
)= sin(
sin(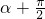 )=
)= cosα=
cosα= ,
,∴cosα=
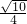 ,又因为α∈[0,
,又因为α∈[0, ],∴sinα=
],∴sinα= …(8分)
…(8分)同理可得f(
 +π)=
+π)= sin(2(
sin(2(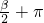 )+
)+ )=
)= sin(
sin(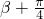 )=
)= ,…(9分)
,…(9分)又因为β∈[0,
 ],∴
],∴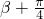 ∈[
∈[ ,
, ],∴
],∴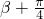 =
= ,解得β=
,解得β= …(11分)
…(11分)∴sin(α+β)=sin(
 )=sinαcos
)=sinαcos +cosαsin
+cosαsin =
=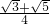 …(12分)
…(12分)分析:(1)由三角函数的运算可得f(x)=
 sin(2x+
sin(2x+ ),易得最值和周期;
),易得最值和周期;(2)由题意可得cosα=
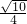 ,进而可得sinα=
,进而可得sinα= ,同理可得β=
,同理可得β= ,进而可得sin(α+β)=sin(
,进而可得sin(α+β)=sin( ),代入数值计算即可.
),代入数值计算即可.点评:本题考查三角函数的化简和求值,涉及函数的周期和最值的求解,属中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
已知函数f(x)=
,则关于x的方程f2(x)+bf(x)+c=0有5个不同实数解的充要条件是( )
|
| A、b<-2且c>0 |
| B、b>-2且c<0 |
| C、b<-2且c=0 |
| D、b≥-2且c=0 |
 已知函数f(x)的图象如图所示,则函数的值域为( )
已知函数f(x)的图象如图所示,则函数的值域为( )