题目内容
已知△ABC中,内角A,B,C所对的边分别是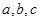 ,AD⊥BC于D,则有
,AD⊥BC于D,则有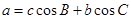 ,类比上述推理结论,写出下列条件下的结论:四面体P—ABC中,△ABC、△PAB、△PBC、△PCA的面积分别为S、S1、S2、S3,二面角P—AB—C、P—BC—A、P—AC—B的度数分别为
,类比上述推理结论,写出下列条件下的结论:四面体P—ABC中,△ABC、△PAB、△PBC、△PCA的面积分别为S、S1、S2、S3,二面角P—AB—C、P—BC—A、P—AC—B的度数分别为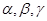 ,则S=_________________________________________.
,则S=_________________________________________.
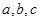 ,AD⊥BC于D,则有
,AD⊥BC于D,则有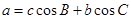 ,类比上述推理结论,写出下列条件下的结论:四面体P—ABC中,△ABC、△PAB、△PBC、△PCA的面积分别为S、S1、S2、S3,二面角P—AB—C、P—BC—A、P—AC—B的度数分别为
,类比上述推理结论,写出下列条件下的结论:四面体P—ABC中,△ABC、△PAB、△PBC、△PCA的面积分别为S、S1、S2、S3,二面角P—AB—C、P—BC—A、P—AC—B的度数分别为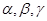 ,则S=_________________________________________.
,则S=_________________________________________. 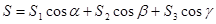
这是一个类比推理的题,在由平面图形到空间图形的类比推理中,一般是由点的性质类比推理到线的性质,由线的性质类比推理到面的性质,由已知在平面几何中,若△ABC中,如果点A在BC边上的射影是D,△ABC的三边BC、AC、AB的长依次是a、b、c,则a=b?cosC+c?cosb,我们可以类比这一性质,推理出若四面体P-ABC中,△ABC、△PAB、△PBC、△PCA的面积依次为S、S1、S2、S3,二面角P-AB-C、P-BC-A、P-CA-B的度数依次为α、β、γ,则S=S1cosα+S2cosβ+S3cosγ.
解答:解:由已知在平面几何中,
在△ABC中,如果点A在BC边上的射影是D,△ABC的三边BC、AC、AB的长依次是a、b、c,则a=b?cosC+c?cosb,
我们可以类比这一性质,推理出:
若四面体P-ABC中,△ABC、△PAB、△PBC、△PCA的面积依次为S、S1、S2、S3,
二面角P-AB-C、P-BC-A、P-CA-B的度数依次为α、β、γ,则S=S1cosα+S2cosβ+S3cosγ.
故答案为:S1cosα+S2cosβ+S3cosγ.
解答:解:由已知在平面几何中,
在△ABC中,如果点A在BC边上的射影是D,△ABC的三边BC、AC、AB的长依次是a、b、c,则a=b?cosC+c?cosb,
我们可以类比这一性质,推理出:
若四面体P-ABC中,△ABC、△PAB、△PBC、△PCA的面积依次为S、S1、S2、S3,
二面角P-AB-C、P-BC-A、P-CA-B的度数依次为α、β、γ,则S=S1cosα+S2cosβ+S3cosγ.
故答案为:S1cosα+S2cosβ+S3cosγ.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
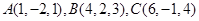 ,则
,则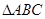 的形状是
的形状是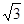 ,则
,则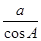 =
= 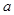 、
、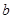 、
、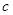 ,若三角形ABC的面积
,若三角形ABC的面积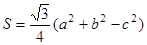 ,则C=
,则C=  海里/时的速度追赶,要在最短的时间内追上走私船,则缉私船应沿北偏东 的方向航行。
海里/时的速度追赶,要在最短的时间内追上走私船,则缉私船应沿北偏东 的方向航行。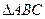 中,
中, ,
,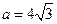 ,
, ,则
,则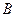 等于 ( )
等于 ( )  或
或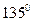
 ,则∠A=
,则∠A= 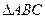 中,AB=2,BC=3,
中,AB=2,BC=3,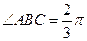 ,若使
,若使