题目内容
定义在R上的偶函数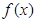 ,对任意x1,x2∈[0,+∞),(x1≠x2),有
,对任意x1,x2∈[0,+∞),(x1≠x2),有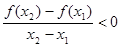 ,
,
则 ( )
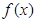 ,对任意x1,x2∈[0,+∞),(x1≠x2),有
,对任意x1,x2∈[0,+∞),(x1≠x2),有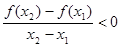 ,
, 则 ( )
A.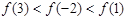 | B.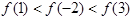 |
C.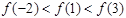 | D.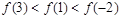 |
A
试题分析:∵任意x1,x2∈[0,+∞),(x1≠x2),有
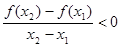 ,∴函数f(x)在[0,+∞)单调递减,∵3>2>1,∴f(3)<f(2)<f(1),又函数
,∴函数f(x)在[0,+∞)单调递减,∵3>2>1,∴f(3)<f(2)<f(1),又函数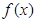 为偶函数,∴f(-2)="f(2)" ,∴
为偶函数,∴f(-2)="f(2)" ,∴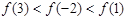 ,故选A
,故选A点评:熟练掌握函数的单调性和奇偶性是解决此类问题的关键,属基础题

练习册系列答案
相关题目
 )=( )
)=( )

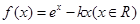
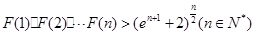 .
.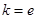 ,试确定函数
,试确定函数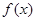 的单调区间;
的单调区间;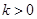 且对任意
且对任意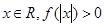 恒成立,试确定实数
恒成立,试确定实数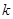 的取值范围;
的取值范围;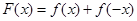 ,求证:
,求证: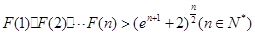 .
.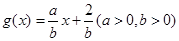 和函数
和函数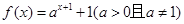 的图象恒过同一个定点,则
的图象恒过同一个定点,则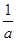 +
+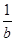 的最小值为________.
的最小值为________.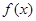 的图象是连续不断的,且有如下对应值表:
的图象是连续不断的,且有如下对应值表:


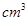 ,高为2
,高为2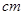 长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省?
长方体的无盖铁盒,问这个铁盒底面的长和宽各为多少时材料最省? 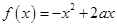 与
与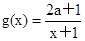 在区间[1,2]上都是减函数,则a的取值范围是
在区间[1,2]上都是减函数,则a的取值范围是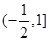



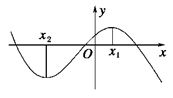
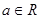 ,若关于
,若关于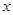 的方程
的方程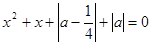 有实根,则
有实根,则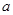 的取值范围是____.
的取值范围是____.