题目内容
已知数列｛a
｝满足a=n+
，若对所有n
N
不等式a≥a
恒成立，则实数c的取值范围是_____________；
6≤c≤12
解析试题分析：根据对所有n∈N*不等式an≥a3恒成立，可得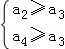
，验证可知数列在（1，2）上递减，（3，+∞）上递增，或在（1，3）上递减，（4，+∞）上递增．
解：由题意，c＞0，
∵对所有n∈N*不等式an≥a3恒成立，
∴
∴
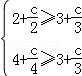
∴6≤c≤12
此时，数列在（1，2）上递减，（3，+∞）上递增，或在（1，3）上递减，（4，+∞）上递增
故答案为：6≤c≤12
考点：数列的函数特性
点评：本题考查数列中的恒成立问题，考查学生的计算能力，属于基础题．
练习册系列答案
相关题目
中，若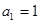
，
，则该数列的通项
________________.
的前
项和
，则数列
=
，数列
满足
，则数列
的通项公式是 .
的首项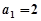
，且对任意的
都有
，则
。
，则
；
；
，则
一定有最小值．
的前
项和
，则
= 
=p（p为正常数，n∈N+），则称{an}为“等方比数列”.