题目内容
已知函数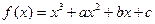 图像上一点
图像上一点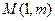 处的切线方程为
处的切线方程为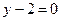 ,其中
,其中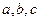 为常数.
为常数.
(Ⅰ)函数 是否存在单调减区间?若存在,则求出单调减区间(用
是否存在单调减区间?若存在,则求出单调减区间(用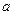 表示);
表示);
(Ⅱ)若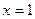 不是函数
不是函数 的极值点,求证:函数
的极值点,求证:函数 的图像关于点
的图像关于点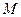 对称.
对称.
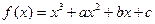 图像上一点
图像上一点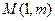 处的切线方程为
处的切线方程为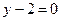 ,其中
,其中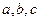 为常数.
为常数.(Ⅰ)函数
 是否存在单调减区间?若存在,则求出单调减区间(用
是否存在单调减区间?若存在,则求出单调减区间(用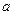 表示);
表示);(Ⅱ)若
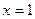 不是函数
不是函数 的极值点,求证:函数
的极值点,求证:函数 的图像关于点
的图像关于点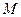 对称.
对称.(Ⅰ)当 时,
时,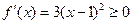 ,函数
,函数 在区间
在区间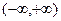 上单调增增,不存在单调减区间;
上单调增增,不存在单调减区间;
当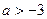 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为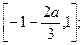
当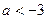 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为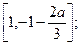
(Ⅱ)证明见解析
 时,
时,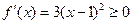 ,函数
,函数 在区间
在区间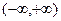 上单调增增,不存在单调减区间;
上单调增增,不存在单调减区间; 当
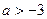 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为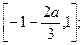
当
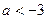 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为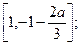
(Ⅱ)证明见解析
(Ⅰ)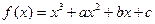 ,
,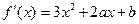 , ……………1分
, ……………1分
由题意,知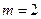 ,
,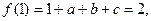
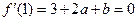 ,
,
即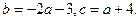 ……………………2分
……………………2分
 …………………3分
…………………3分
① 当 时,
时,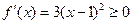 ,函数
,函数 在区间
在区间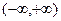 上单调增加,
上单调增加,
不存在单调减区间; ……………………5分
② 当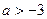 时,
时,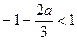 ,有
,有
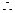 当
当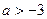 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为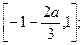 ……………7分
……………7分
③ 当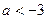 时,
时,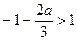 ,有
,有
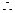 当
当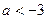 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为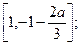 …………9分
…………9分
(Ⅱ)由(Ⅰ)知:若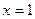 不是函数
不是函数 的极值点,则
的极值点,则 ,
,
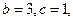
 …………………10分
…………………10分
设点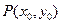 是函数
是函数 的图像上任意一点,则
的图像上任意一点,则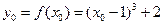 ,
,
点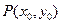 关于点
关于点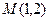 的对称点为
的对称点为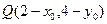 ,
,
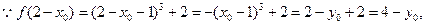
(或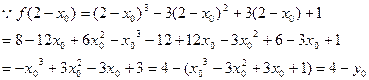 )
)
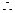 点
点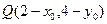 在函数
在函数 的图像上.
的图像上.
由点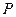 的任意性知函数
的任意性知函数 的图像关于点
的图像关于点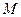 对称. …………………14分
对称. …………………14分
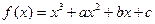 ,
,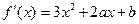 , ……………1分
, ……………1分由题意,知
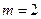 ,
,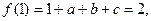
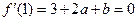 ,
,即
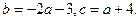 ……………………2分
……………………2分 …………………3分
…………………3分① 当
 时,
时,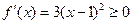 ,函数
,函数 在区间
在区间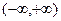 上单调增加,
上单调增加,不存在单调减区间; ……………………5分
② 当
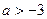 时,
时,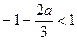 ,有
,有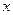 | 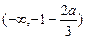 | 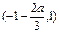 | 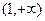 |
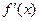 | + | - | + |
 | 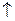 |  | 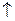 |
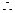 当
当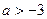 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为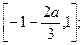 ……………7分
……………7分③ 当
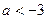 时,
时,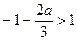 ,有
,有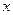 | 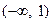 | 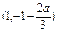 | 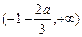 |
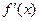 | + | - | + |
 | 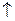 |  | 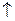 |
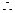 当
当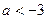 时,函数
时,函数 存在单调减区间,为
存在单调减区间,为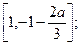 …………9分
…………9分(Ⅱ)由(Ⅰ)知:若
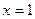 不是函数
不是函数 的极值点,则
的极值点,则 ,
,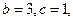
 …………………10分
…………………10分设点
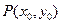 是函数
是函数 的图像上任意一点,则
的图像上任意一点,则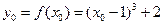 ,
,点
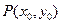 关于点
关于点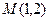 的对称点为
的对称点为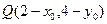 ,
,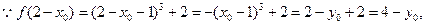
(或
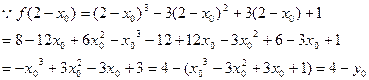 )
)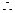 点
点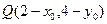 在函数
在函数 的图像上.
的图像上.由点
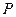 的任意性知函数
的任意性知函数 的图像关于点
的图像关于点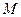 对称. …………………14分
对称. …………………14分
练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 的图像关于原点对称,其中m,n为实常数。
的图像关于原点对称,其中m,n为实常数。 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。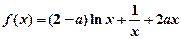 (a∈R).
(a∈R).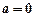 时,求
时,求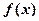 的极值;
的极值;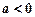 时,求
时,求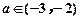 及
及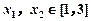 ,恒有
,恒有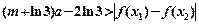
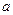 、
、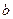 、
、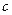 都是实数,函数
都是实数,函数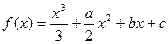 的导函数为
的导函数为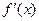
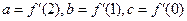 ,求函数
,求函数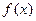 的解析式;
的解析式;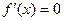 的两个实数根分别为
的两个实数根分别为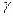 、
、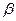 ,并且
,并且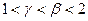
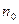 ,使得
,使得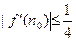 ?请说明理由.
?请说明理由.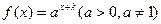 的图象过(-1,1)点,其反函数
的图象过(-1,1)点,其反函数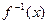 的图象过(8,2)点。
的图象过(8,2)点。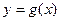 的图象,写出
的图象,写出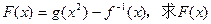 的最小值及取最小值时x的值。
的最小值及取最小值时x的值。 ,
, ,函数
,函数 的图象与
的图象与 轴的交点也在函数
轴的交点也在函数 的图象上,且在此点有公共切线.
的图象上,且在此点有公共切线. 、
、 的值;
的值; 的大小.
的大小.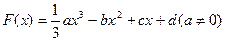 的图象过原点,
的图象过原点,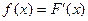 ,
,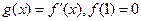 ,函数y=f(x)与y=g(x)的图象交于不同两点A、B。
,函数y=f(x)与y=g(x)的图象交于不同两点A、B。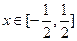 ,求线段AB在x轴上的射影长的取值范围;
,求线段AB在x轴上的射影长的取值范围; cos2t+
cos2t+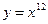 ;(2)
;(2)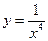 ;(3)
;(3)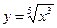 .
.