题目内容
已知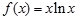 .
. .
.
(1)求函数 在区间
在区间 上的最小值;
上的最小值;
(2)对一切实数 ,
,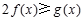 恒成立,求实数
恒成立,求实数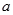 的取值范围;
的取值范围;
(3) 证明对一切 ,
,  恒成立.
恒成立.
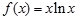 .
. .
.(1)求函数
 在区间
在区间 上的最小值;
上的最小值;(2)对一切实数
 ,
,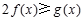 恒成立,求实数
恒成立,求实数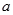 的取值范围;
的取值范围;(3) 证明对一切
 ,
,  恒成立.
恒成立.(1)见解析;(2)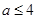 ;(3)见解析.
;(3)见解析.
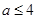 ;(3)见解析.
;(3)见解析.试题分析:(1)对于研究非常规的初等函数的最值问题,往往都需要求函数的导数.根据函数导数的正负判断函数的单调性,利用单调性求函数在某个区间上的最值;(2)恒成立问题,一般都需要将常数和变量分离开来(分离常数法)转化为最值问题处理;(3)证明不等式
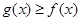 恒成立问题,往往将不等式转化为函数
恒成立问题,往往将不等式转化为函数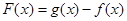 来证明
来证明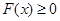 恒成立问题.但有些时候这样转化后不等会乃然很难实现证明,还需对不等式经行恒等变形以达到化简不等式的目的,然后再证.
恒成立问题.但有些时候这样转化后不等会乃然很难实现证明,还需对不等式经行恒等变形以达到化简不等式的目的,然后再证.试题解析:⑴
 ,当
,当 ,
,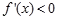 ,
, 单调递减,
单调递减,当
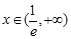 ,
,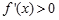 ,
, 单调递增. 1分
单调递增. 1分(由于
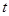 的取值范围不同导致
的取值范围不同导致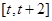 所处的区间函数单调性不同,故对
所处的区间函数单调性不同,故对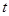 经行分类讨论.)
经行分类讨论.)①
 ,t无解; 2分
,t无解; 2分②
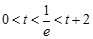 ,即
,即 时,
时,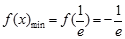 3分
3分③
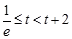 ,即
,即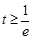 时,
时, 在
在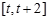 上单调递增,
上单调递增, ;
; 所以
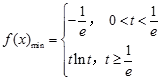 5分
5分由题可知:
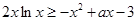 ,则
,则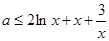 .因对于
.因对于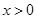 ,
,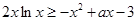 恒成立,故
恒成立,故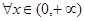 ,
,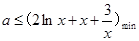
设
 ,则
,则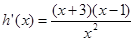 .
.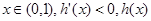 单调递增,
单调递增,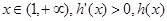 单调递减.
单调递减.所以
 ,即
,即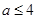 .
.问题等价于证明
 (为了利用第(1)小问结论,并考虑到作差做函数证明不方便,下证
(为了利用第(1)小问结论,并考虑到作差做函数证明不方便,下证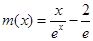 的最值与
的最值与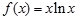 最值的关系.)
最值的关系.)由(1)可知
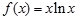 在
在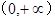 的最小值是
的最小值是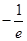 ,当且仅当
,当且仅当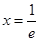 时取到.
时取到.设
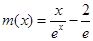 ,则
,则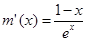 ,易得
,易得 ,当且仅当
,当且仅当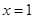 时取到.
时取到.从而对于一切
 ,都有
,都有 恒成立.
恒成立.
练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
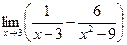
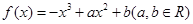 图象上任意一点处的切线的斜率都小于1,则实数a的取值范围是______.
图象上任意一点处的切线的斜率都小于1,则实数a的取值范围是______. 为函数
为函数 与
与
 图象的公共点,以
图象的公共点,以 与两曲线都相切,则实数
与两曲线都相切,则实数 的最大值为 .
的最大值为 .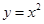 在点
在点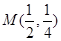 处的切线的倾斜角是 ( )
处的切线的倾斜角是 ( )

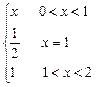 则f(x)的连续区间为( )
则f(x)的连续区间为( )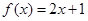 ,则
,则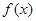 在区间
在区间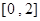 上的平均变化率为 .
上的平均变化率为 .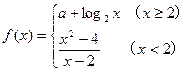 在x=2处连续,则常数
在x=2处连续,则常数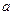 的值是 ( )
的值是 ( )