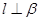题目内容
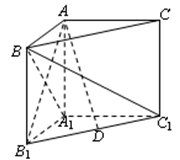
如图,在直三棱柱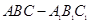 中,
中,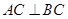 ,点D是AB的中点,
,点D是AB的中点,
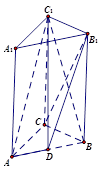
求证:(1)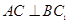 ; (2)
; (2)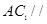 平面
平面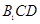
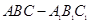 中,
中,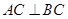 ,点D是AB的中点,
,点D是AB的中点,
求证:(1)
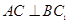 ; (2)
; (2)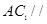 平面
平面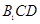
(1)详见解析;(2)详见解析.
试题分析:(1)证明两条直线垂直,只需证明直线和平面垂直,由题知
 面
面 ,从而
,从而 ,又
,又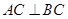 ,
,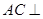 面
面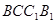 ,从而
,从而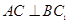 ;(2)证明直线和平面平行,一般有两种方法,其一利用直线和平面平行的判定定理(在平面内找一条直线和已知直线平行);其二利用面面平行的性质(如果两个平面平行,则一个平面内的任意一条直线和另一个平面平行),设
;(2)证明直线和平面平行,一般有两种方法,其一利用直线和平面平行的判定定理(在平面内找一条直线和已知直线平行);其二利用面面平行的性质(如果两个平面平行,则一个平面内的任意一条直线和另一个平面平行),设 ,连接
,连接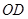 ,则
,则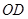 ∥
∥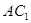 ,从而说明
,从而说明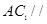 平面
平面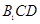 .
.试题解析:(1)在直三棱柱ABC-A1B1C1中,C1C⊥平面ABC,又由于AC
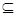 平面ABC,所以CC1⊥AC.
平面ABC,所以CC1⊥AC.又因为AC⊥BC BC
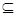 平面BCC1B1 CC1
平面BCC1B1 CC1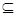 平面BCC1B1 BC1
平面BCC1B1 BC1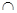 CC1=C,所以AC⊥平面BCC1B1,又因为BC1
CC1=C,所以AC⊥平面BCC1B1,又因为BC1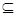 平面BCC1B1 所以AC⊥BC1 5分
平面BCC1B1 所以AC⊥BC1 5分(2)设BC1
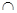 B1C=O,连OD,则O为BC1中点,又∵D是AB中点,∴OD是△ABC1的中位线,∴OD∥AC1,,又∵OD
B1C=O,连OD,则O为BC1中点,又∵D是AB中点,∴OD是△ABC1的中位线,∴OD∥AC1,,又∵OD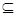 平面B1CD1, AC1
平面B1CD1, AC1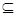 平面B1CD ∴AC1∥平面B1CD 10分
平面B1CD ∴AC1∥平面B1CD 10分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
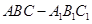 中,
中,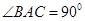 ,
,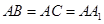 .
.
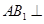 平面
平面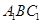 ;
;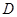 为
为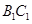 的中点,求
的中点,求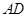 与平面
与平面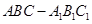 中,
中,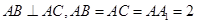 ,点
,点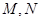 分别为
分别为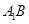 和
和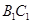 的中点.
的中点.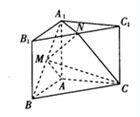
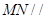 平面
平面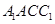 ;
;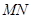 和
和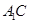 所成的角.
所成的角. ,E、F分别是BC、AP的中点.
,E、F分别是BC、AP的中点.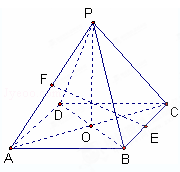
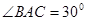 ,
,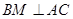 交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,
交AC于点M,EA⊥平面ABC,FC∥EA,AC=4,EA=3,FC=1,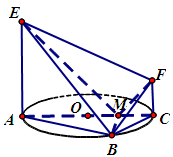
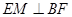 ;
;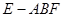 的体积
的体积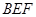 和平面
和平面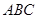 所成的锐二面角的正切值.
所成的锐二面角的正切值.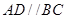 ,
,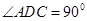 ,平面
,平面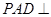 底面
底面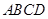 ,
,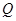 为
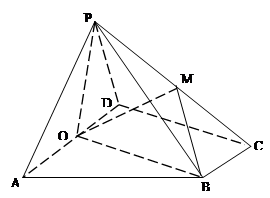
为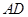 中点,M是棱PC上的点,
中点,M是棱PC上的点,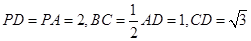 .
.
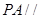 平面
平面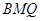 ;
;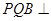 底面
底面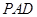 ;
;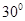 ,设PM=tMC,试确定t的值.
,设PM=tMC,试确定t的值.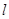 为直线,
为直线,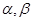 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )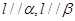 ,则
,则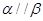
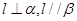 ,则
,则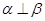
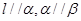 ,则
,则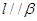
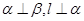 ,则
,则