题目内容
已知函数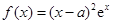 在
在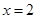 时取得极小值.
时取得极小值.
(1)求实数 的值;
的值;
(2)是否存在区间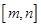 ,使得
,使得 在该区间上的值域为
在该区间上的值域为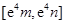 ?若存在,求出
?若存在,求出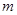 ,
,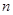 的值;
的值;
若不存在,说明理由.
(1) ,(2)满足条件的
,(2)满足条件的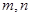 值只有一组,且
值只有一组,且 .
.
解析试题分析:(1)根据函数极值求参数,不要忘记列表检验.因为导数为零的点不一定是极值点. 因为 ,所以由题意
,所以由题意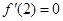 ,解得
,解得 或
或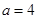 .当
.当 时,
时, 在
在 上为减函数,在
上为减函数,在 上为增函数,符合题意;当
上为增函数,符合题意;当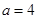 时,
时, 在
在 上为增函数,在
上为增函数,在 ,
, 上为减函数,不符合题意.(2)由值域范围确定解析式中参数范围,是函数中难点.主要用到分类讨论的思想方法.首先因为
上为减函数,不符合题意.(2)由值域范围确定解析式中参数范围,是函数中难点.主要用到分类讨论的思想方法.首先因为 ,所以
,所以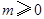 .① 若
.① 若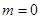 ,则
,则 ,因为
,因为 ,所以
,所以 .设
.设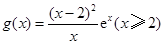 ,则
,则 ,所以
,所以 在
在 上为增函数.由于
上为增函数.由于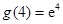 ,即方程
,即方程 有唯一解为
有唯一解为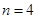 .② 若
.② 若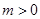 ,则
,则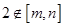 ,即
,即 或
或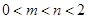 .
.
(Ⅰ) 时,
时, ,由①可知不存在满足条件的
,由①可知不存在满足条件的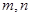 .(Ⅱ)
.(Ⅱ)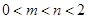 时,
时,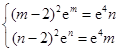 ,两式相除得
,两式相除得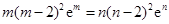 .设
.设 ,则
,则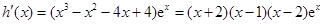 ,
, 在
在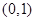 递增,在
递增,在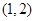 递减,由
递减,由 得
得 ,
,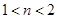 ,此时
,此时 ,矛盾.
,矛盾.
【解】(1) ,
,
由题意知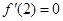 ,解得
,解得 或
或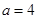 . 2分
. 2分
当 时,
时,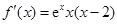 ,
,
易知 在
在 上为减函数,在
上为减函数,在 上为增函数,符合题意;
上为增函数,符合题意;
当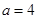 时,
时,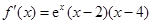 ,
,
易知 在
在 上为增函数,在
上为增函数,在 ,
, 上为减函数,不符合题意.
上为减函数,不符合题意.
所以,满足条件的 . 5分
. 5分
(2)因为 ,所以
,所以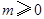 . &n
. &n

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,其中e为自然对数的底数.
,其中e为自然对数的底数.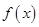 是增函数,求实数
是增函数,求实数 的取值范围;
的取值范围; 时,求函数
时,求函数 上的最小值;
上的最小值; .
.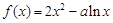 .
.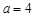 ,求函数
,求函数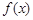 的极小值;
的极小值;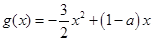 ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量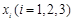 使得
使得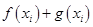 的值相等,若存在,请求出
的值相等,若存在,请求出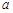 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?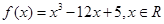 .
.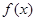 的单调区间和极值;
的单调区间和极值;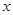 的方程
的方程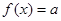 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.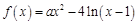 ,
,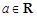 .
.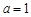 时,求
时,求 的单调区间;
的单调区间;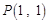 和函数
和函数 ,对任意
,对任意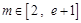 ,直线
,直线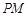 倾斜角都是钝角,求
倾斜角都是钝角,求 的取值范围.
的取值范围.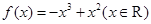 ,
, 满足
满足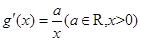 ,且
,且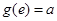 ,
, 为自然对数的底数.
为自然对数的底数.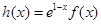 ,求
,求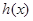 在
在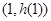 处的切线方程;
处的切线方程;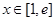 ,使得
,使得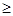
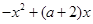 成立,求
成立,求 的取值范围;
的取值范围;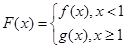 ,
, 为坐标原点,若对于
为坐标原点,若对于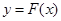 在
在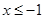 时的图象上的任一点
时的图象上的任一点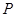 ,在曲线
,在曲线 上总存在一点
上总存在一点 ,使得
,使得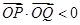 ,且
,且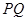 的中点在
的中点在 轴上,求
轴上,求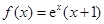 .
.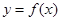 在点
在点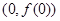 处的切线方程;
处的切线方程;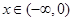 ,都有
,都有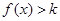 ,求
,求 的取值范围.
的取值范围.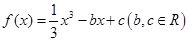 .
.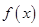 在点
在点 处的切线方程为
处的切线方程为 ,求
,求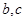 的值;
的值; ,函数
,函数 在区间
在区间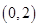 内有唯一零点,求
内有唯一零点,求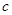 的取值范围;
的取值范围;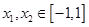 ,均有
,均有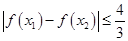 ,求
,求 的取值范围.
的取值范围.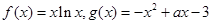 .
. 在
在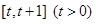 上的最小值;
上的最小值; 恒成立,求实数
恒成立,求实数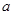 的取值范围;
的取值范围;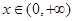 ,都有
,都有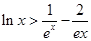 成立.
成立.