题目内容
（不等式选做题）已知函数f（x）=|2x+1|，g（x）=|x|+a．若存在x∈R，使得f（x）≤g（x）成立，则实数a的取值范围为 ．
【答案】分析：先由f（x）≤g（x）分离出参数a得a≥|2x+1|-|x|，令h（x）=|2x+1|-|x|，下面求得h（x）的最小值，从而所求实数a的范围．
解答：解：由f（x）≤g（x）得a≥|2x+1|-|x|，
令h（x）=|2x+1|-|x|，则 h（x）=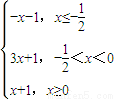
（7分）
故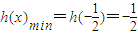
，从而所求实数a的范围为 
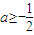（10分）
故答案为：[-
，+∞]
点评：题主要考查了绝对值不等式的解法、函数存在性问题．对于函数存在性问题，处理的方法是：利用分离参数法转化为求函数的最值问题解决．
解答：解：由f（x）≤g（x）得a≥|2x+1|-|x|，
令h（x）=|2x+1|-|x|，则 h（x）=
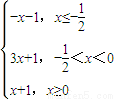（7分）故
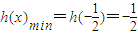，从而所求实数a的范围为 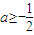（10分）故答案为：[-
，+∞]点评：题主要考查了绝对值不等式的解法、函数存在性问题．对于函数存在性问题，处理的方法是：利用分离参数法转化为求函数的最值问题解决．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
选做题（考生只能从A，B，C中选做一题，多做以所做第一题记分）
+ 
)≥9对任意正实数x,y恒成立,则正实数a的最小值为_____.