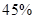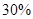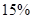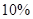题目内容
为了调查学生的视力情况,随机抽查了一部分学生的视力,将调查结果分组,分组区间为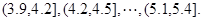 ,经过数据处理,得到如下频率分布表
,经过数据处理,得到如下频率分布表
(Ⅰ)求频率分布表中未知量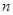 ,
,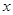 ,
,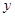 ,
,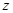 的值
的值
(Ⅱ)从样本中视力在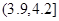 和
和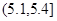 的所有同学中随机抽取两人,求两人视力差的绝对值低于
的所有同学中随机抽取两人,求两人视力差的绝对值低于 的概率
的概率
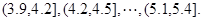 ,经过数据处理,得到如下频率分布表
,经过数据处理,得到如下频率分布表| 分组 | 频数 | 频率 |
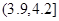 | 3 | 0.06 |
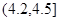 | 6 | 0.12 |
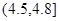 | 25 | 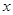 |
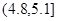 | 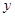 | 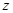 |
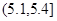 | 2 | 0.04 |
| 合计 | 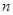 | 1.00 |
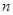 ,
,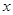 ,
,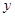 ,
,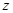 的值
的值(Ⅱ)从样本中视力在
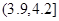 和
和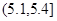 的所有同学中随机抽取两人,求两人视力差的绝对值低于
的所有同学中随机抽取两人,求两人视力差的绝对值低于 的概率
的概率(Ⅰ)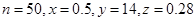 ;(Ⅱ)两人的视力差的绝对值低于
;(Ⅱ)两人的视力差的绝对值低于 的概率为
的概率为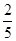 .
.
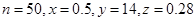 ;(Ⅱ)两人的视力差的绝对值低于
;(Ⅱ)两人的视力差的绝对值低于 的概率为
的概率为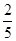 .
.试题分析:(I)根据题意,由(5.1,5.4]一组频数为2,频率为0.04,可得
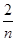 =0.04,解可得n的值,进而由x=
=0.04,解可得n的值,进而由x=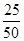 =0.5,可得x的值,由频数之和为50,可得y的值,由频率、频数的关系可得z的值;
=0.5,可得x的值,由频数之和为50,可得y的值,由频率、频数的关系可得z的值;(II)设样本视力在(3.9,4.2]的3人为a,b,c,样本视力在(5.1,5.4]的2人为d,e;由题意列举从5人中任取两人的基本事件空间Ω,可得其基本事件的数目,设事件A表示“抽取的两人的视力差的绝对值低于0.5”,由Ω可得基本事件数目,由等可能事件的概率,计算可得答案.
试题解析:(Ⅰ)由频率分布表可知,样本容量为n,由
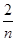 =0.04,得n=50 (2分)
=0.04,得n=50 (2分)∴x=
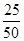 =0.5, y=50-3-6-25-2=14,z=
=0.5, y=50-3-6-25-2=14,z=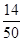 =0.28 (4分)
=0.28 (4分)(Ⅱ)记样本中视力在(3.9,4.2]的三个人为a,b,c,在(5.1,5.4]的2人为d,e.
由题意,从5人中随机抽取两人,所有结果有:{a,b},{a,c},{a,d},{a,e},{b,c},
{b,d},{b,e},{c,d},{c,e},共10种. (7分)
设事件A表示“两人的视力差的绝对值低于0.5”,则事件A包含的可能结果有:{a,b},
{a,c},{b,c},{d,e},共4种. (9分)
P(A)=
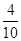 =
=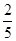 .故两人的视力差的绝对值低于0.5的概率为
.故两人的视力差的绝对值低于0.5的概率为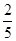 . (12分)
. (12分)
练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
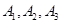 通晓日语,
通晓日语, 通晓俄语,
通晓俄语,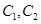 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.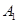 被选中的概率;(5分);(2)求
被选中的概率;(5分);(2)求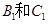 不全被选中的概率.(5分)
不全被选中的概率.(5分)

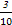

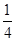 ,得到B公司面试的概率为p,且两个公司是否让其面试是独立的,记X为小王得到面试的公司个数.若X=0时的概率P(X=0)=
,得到B公司面试的概率为p,且两个公司是否让其面试是独立的,记X为小王得到面试的公司个数.若X=0时的概率P(X=0)=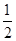 ,则随机变量X的数学期望为________.
,则随机变量X的数学期望为________.
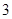 位教师安排在周一至周五中的
位教师安排在周一至周五中的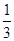
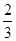
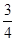
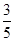
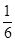
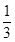
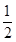
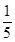
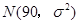 ,其中
,其中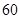 分以下的考生人数占
分以下的考生人数占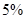 ,则数学成绩在
,则数学成绩在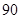 至
至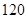 分之间的考生人数所占百分比约为 ( )
分之间的考生人数所占百分比约为 ( )