题目内容
16．已知函数f（x）的定义域为R，若f（a）•f（b）＜0，则（ ）| A． | 函数f（x）在区间[a，b]内一定有零点 | B． | 函数f（x）在区间[a，b]内不一定有零点 | ||
| C． | 函数f（x）在区间[a，b]内有唯一零点 | D． | 函数f（x）在区间[a，b]内没有零点 |
分析 利用零点存在性定理，即可得出结论．
解答 解：函数f（x）的定义域为R，若f（a）•f（b）＜0，则函数f（x）在区间[a，b]内不一定有零点，
故选：B．
点评 本题考查零点存在性定理，考查学生分析解决问题的能力，比较基础．
练习册系列答案
阳光试卷单元测试卷系列答案
相关题目
6．若（a-2i）i2013=b-i，其中a，b∈R，i是虚数单位，则a2+b2等于（ ）
| A． | 0 | B． | 2 | C． | $\frac{5}{2}$ | D． | 5 |
4．已知函数f（x）=x2+ax+1，若存在x0，使|f（x0）|$≤\frac{1}{4}$，|f（x0+1）|≤$\frac{1}{4}$同时成立，则a的取值范围是（ ）
| A． | [4，6] | B． | [-$\sqrt{6}$，-2] | C． | [2，$\sqrt{6}$] | D． | [-$\sqrt{6}$，-2]∪[2，$\sqrt{6}$] |
8．函数f（x）=Asin（wx+φ）（A＞0，w＞0，-$\frac{π}{2}$＜φ＜$\frac{π}{2}$）的部分图象如图所示，则f（$\frac{3π}{2}$）的值是（ ）
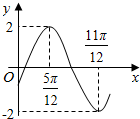
| A． | -1 | B． | 1 | C． | -$\sqrt{3}$ | D． | $\sqrt{3}$ |