题目内容
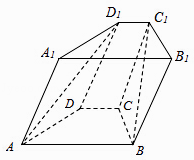
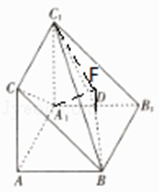
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D是A1B1的中点. 
(1)求证:A1C∥平面BDC1;
(2)若AB⊥AC,且AB=AC= ![]() AA1 , 求二面角A﹣BD﹣C1的余弦值.
AA1 , 求二面角A﹣BD﹣C1的余弦值.
【答案】
(1)证明:(1)取AB的中点E,连结A1E,CE,DE,
在四边形A1EBD是平行四边形,即A1E∥BD,
同理,四边形CC1DE是平行四边形,即CE∥C1D,
又A1E∩CE=E,∴平面A1CE∥平面BDC1,
∵A1C平面A1CE,∴A1C∥平面BDC1
(2)解:法一:延长BD至F,连结A1F,使得A1F⊥DF,连结C1F,
∵AB⊥AC,∴A1B⊥A1C,
又A1C1⊥AA1,∴A1C1⊥平面AA1B1B,∴∠A1FC1是所求二面角的平面角,
设AB=2,又AB=AC= ![]() ,∴A1D=1,AA1=3,∴BD=
,∴A1D=1,AA1=3,∴BD= ![]() ,
,
∵△A1DF∽△BDB1,∴ ![]() ,∴A1F=
,∴A1F= ![]() ,
,
∵A1C1=2,∴ ![]() ,
,
∴cos∠A1FC1= ![]() =
= ![]() .∴二面角A﹣BD﹣C1的余弦值为
.∴二面角A﹣BD﹣C1的余弦值为 ![]() .
.
法二:棱柱ABC﹣A1B1C1是直三棱柱,A1B1⊥A1C1,
∴A1B1,A1C1,AA1两两垂直,
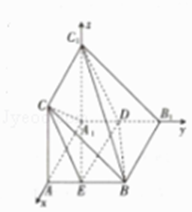
以A1为坐标原点,建立如图所求的空间直角坐标系A1﹣xyz,
设AB=2,则B(3,2,0),D(0,1,0),C1(0,0,2),
∴ ![]() =(3,1,0),
=(3,1,0), ![]() =(0,﹣1,2),
=(0,﹣1,2),
设平面BDC1的法向量 ![]() =(x,y,z),
=(x,y,z),
则 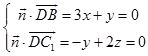 ,取y=6,得
,取y=6,得 ![]() =(﹣2,6,3),
=(﹣2,6,3),
∵平面AA1DB的一个法向量 ![]() =(0,0,1)
=(0,0,1)
∴cos< ![]() >=
>= ![]() =
= ![]() ,
,
由图知二面角A﹣BD﹣C1的平面角为多姿多彩锐角,
∴二面角A﹣BD﹣C1的余弦值为 ![]() ./p>
./p>
【解析】(1)取AB的中点E,连结A1E,CE,DE,推导出A1E∥BD,CE∥C1D,从而平面A1CE∥平面BDC1,由此能证明A1C∥平面BDC1.(2)法一:延长BD至F,连结A1F,使得A1F⊥DF,连结C1F,推导出∠A1FC1是所求二面角的平面角,由此能求出二面角A﹣BD﹣C1的余弦值.(2)法二:以A1为坐标原点,建立如图所求的空间直角坐标系A1﹣xyz,利用向量法能求出二面角A﹣BD﹣C1的余弦值.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案