题目内容
已知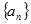 是公差不为零的等差数列,
是公差不为零的等差数列,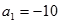 ,且
,且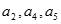 成等比数列.
成等比数列.
(1)求数列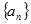 的通项公式;
的通项公式;
(2)若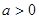 ,求数列
,求数列 的前n项和
的前n项和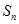 .
.
(1) ,(2)
,(2)
解析试题分析:(1)求等差数列通项,通法是待定系数法. 由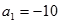 ,及
,及 解得
解得 ,代入等差数列通项公式得:
,代入等差数列通项公式得: ,(2)求数列前n项和,需分析通项公式的结构.因为
,(2)求数列前n项和,需分析通项公式的结构.因为  ,为指数型,其和可利用等比数列前n项和公式
,为指数型,其和可利用等比数列前n项和公式 因此当
因此当 =1时,数列
=1时,数列 的前n项和
的前n项和 ,当
,当 时,
时, ,
, .综上,
.综上,
试题解析:
解:(1)设公差为d,
由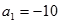 ,且
,且 成等比数列得:
成等比数列得:
因为公差不为零,解得 , 5分
, 5分 7分
7分
(2)由(1)知,
所以
当 =1时,数列
=1时,数列 的前n项和
的前n项和 9分
9分
当 时,令
时,令 ,则
,则 . 10分
. 10分
所以 13分
13分
故 为等比数列,所以
为等比数列,所以 的前n项和
的前n项和 .
.
综上, 16分
16分
考点:等差数列通项,等比数列前n项和公式

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 中,
中,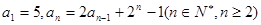 ,若存在实数
,若存在实数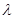 ,使得数列
,使得数列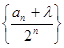 为等差数列,则
为等差数列,则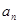 }是等差数列,数列{
}是等差数列,数列{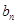 }的前
}的前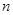 项和
项和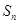 满足
满足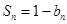 ,
,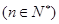 ,且
,且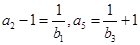
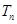 为数列{
为数列{ 中,已知
中,已知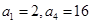 .
. 项和
项和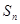 .
.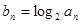 ,求
,求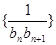 的前
的前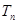 .
. 中,
中,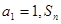 是数列
是数列 项和,对任意
项和,对任意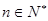 ,有
,有 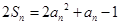 .
.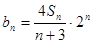 ,求数列
,求数列 的前
的前 .
. )
)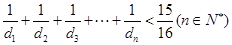 .
.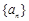 的前
的前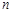 项和为
项和为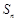 满足
满足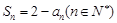 .
.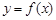 与函数
与函数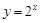 互为反函数,令
互为反函数,令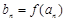 ,求数列
,求数列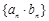 的前
的前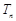 ;
;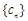 满足
满足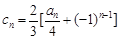 ,证明:对任意的整数
,证明:对任意的整数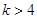 ,有
,有 .
.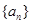 的前
的前 项和
项和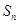 ,满足:
,满足: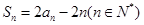 .
.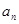 ;
;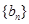 的满足
的满足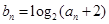 ,
,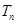 为数列
为数列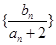 的前
的前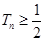 .
.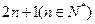 个正整数总和为
个正整数总和为 ,且这些数中后
,且这些数中后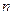 个数的平方和与前
个数的平方和与前 .若
.若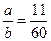 ,则
,则