题目内容
数列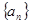
中，
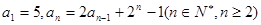，若存在实数
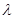，使得数列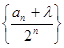
为等差数列，则=
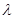解析试题分析：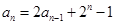
。
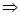
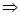
另
，取
，则数列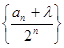为等差数列。
考点：等差数列的定义。
点评：本题关键是观察数列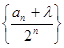的结构，然后把式子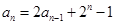变成它的形式。
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
名校名师培优作业本加核心试卷系列答案全程金卷系列答案题目内容
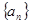数列中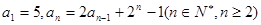，，若存在实数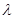，使得数列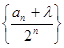为等差数列，则=
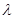解析试题分析：。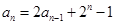
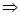
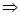
另，取，则数列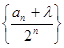为等差数列。
考点：等差数列的定义。
点评：本题关键是观察数列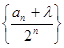的结构，然后把式子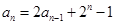变成它的形式。
名校名师培优作业本加核心试卷系列答案全程金卷系列答案
，则
．
，且
，则
=___________
满足
（
）．
可以生成的数列
”是“数列
为单调递增数列，则
；
，其中
，则
一定存在；
第2个数是_________.
满足
，
，则数列
．
成等差数列．
是公差不为零的等差数列，
，且
成等比数列.
,求数列
的前n项和
.