题目内容
若实数a、b、c成等差数列,点P(–1, 0)在动直线l:ax+by+c=0上的射影为M,点N(0, 3),则线段MN长度的最小值是 .
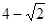
解析试题分析:因为a,b,c成等差数列,所以2b=a+c,即a-2b+c=0,可得方程ax+by+c=0恒过Q(1,-2),
又点P(-1,0)在动直线ax+by+c=0上的射影为M,所以∠PMQ=90°,
所以M在以PQ为直径的圆上,
所以此圆的圆心A坐标为(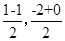 ),即A(0,-1),半径r=
),即A(0,-1),半径r= 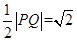 ,
,
又N(0,3),所以|AN|=  ,线段MN长度的最小值是
,线段MN长度的最小值是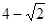 。
。
考点:等差数列的性质;直线关于点、直线对称的直线方程。
点评:此题考查了等差数列的性质,恒过定点的直线方程,圆周角定理,线段中点坐标公式,以及两点间的距离公式,利用等差数列的性质得到2b=a+c,即a-2b+c=0是解本题的突破点.

练习册系列答案
相关题目
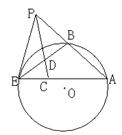
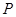 作圆
作圆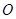 的割线
的割线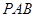 与切线
与切线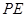 ,
,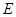 为切点,连接
为切点,连接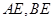 ,
,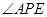 的平分线与
的平分线与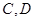 ,若
,若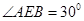 ,则
,则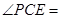 ;
; 
 是抛物线
是抛物线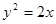 上的动点,点
上的动点,点 轴上的射影是
轴上的射影是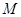 ,
,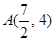 ,则
,则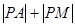 的最小值是 .
的最小值是 .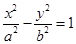 的一条渐近线与抛物线
的一条渐近线与抛物线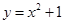 只有一个公共点,则双曲线的离心率为
只有一个公共点,则双曲线的离心率为  被直线l:
被直线l: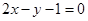 截得的弦长为
截得的弦长为 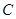 的中心在原点,焦点在
的中心在原点,焦点在 轴上,
轴上,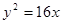 的准线交于
的准线交于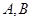 两点,
两点,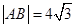 ;则
;则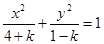 表示双曲线,则
表示双曲线,则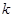 的取值范围是____________.
的取值范围是____________. 轴上, 若其离心率是
轴上, 若其离心率是 焦距是8,则该椭圆的方程
焦距是8,则该椭圆的方程