题目内容
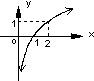10、已知函数y=
|
| A、2x | ||
B、log
| ||
| C、log2（-x） | ||
| D、-log2（-x） |
分析：由函数y=
是偶函数得到图象关于y轴对称．再由f（x）=logax对应的图象过（2，1）求得a，再由x＞0时，f（x）=log2x求得g（x）．
|
解答：解：∵函数y=
是偶函数
∴图象关于y轴对称．
∵f（x）=logax对应的图象过（2，1）
∴a=2
又∵x＞0时，f（x）=log2x
∴x＜0时，f（x）=log2（-x）
即：g（x）=log2（-x）
故选C
|
∴图象关于y轴对称．
∵f（x）=logax对应的图象过（2，1）
∴a=2
又∵x＞0时，f（x）=log2x
∴x＜0时，f（x）=log2（-x）
即：g（x）=log2（-x）
故选C
点评：本题主要考查函数的奇偶性及其图象，特别是常见函数对称性，如：f（x）与f（-x），-f（x）图象关系，及f（|x|），
|f（x）|，|f（|x|）|的图象变化．
|f（x）|，|f（|x|）|的图象变化．
练习册系列答案
名校课堂系列答案
相关题目
已知函数y=f(x+
)为奇函数，设g（x）=f（x）+1，则g(
)+g(
)+g(
)+g(
)+…+g(
)=（ ）
| 1 |
| 2 |
| 1 |
| 2011 |
| 2 |
| 2011 |
| 3 |
| 2011 |
| 4 |
| 2011 |
| 2010 |
| 2011 |
| A、1005 | B、2010 |
| C、2011 | D、4020 |