题目内容
【题目】如图,直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,直线
两点,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,且直线
,且直线![]() 恰好平分
恰好平分![]() .
.

(1)求![]() 的值;
的值;
(2)设![]() 是直线
是直线![]() 上一点,直线
上一点,直线![]() 交抛物线于另一点
交抛物线于另一点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)联立直线的方程和抛物线的方程![]() ,化简写出根与系数关系,由于直线
,化简写出根与系数关系,由于直线![]() 平分
平分![]() ,所以
,所以![]() ,代入点的坐标化简得
,代入点的坐标化简得![]() ,结合跟鱼系数关系,可求得
,结合跟鱼系数关系,可求得![]() ;(2)设
;(2)设![]() ,
,![]() ,
,![]() ,由
,由![]() 三点共线得
三点共线得![]() ,再次代入点的坐标并化简得
,再次代入点的坐标并化简得![]() ,同理由
,同理由![]() 三点共线,可得
三点共线,可得![]() ,化简得
,化简得![]() ,故
,故![]() .
.
试题解析:
(1)由![]() ,整理得
,整理得![]() ,
,
设![]() ,
,![]() ,则
,则 ,
,
因为直线![]() 平分
平分![]() ,∴
,∴![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,得
,得![]() ,满足
,满足![]() ,所以
,所以![]() .
.
(2)由(1)知抛物线方程为![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,
设![]() ,
,![]() ,
,![]() ,由
,由![]() 三点共线得
三点共线得![]() ,
,
所以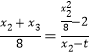 ,即
,即![]() ,
,
整理得:![]() ,①
,①
由![]() 三点共线,可得
三点共线,可得![]() ,②
,②
②式两边同乘![]() 得:
得:![]() ,
,
即:![]() ,③
,③
由①得:![]() ,代入③得:
,代入③得:![]() ,
,
即:![]() ,所以
,所以![]() .
.
所以![]() .
.

练习册系列答案
相关题目
【题目】某社区为了解居民参加体育锻炼的情况,从该社区随机抽取了18名男性居民和12名女性居民,对他们参加体育锻炼的情况进行问卷调查.现按是否参加体育锻炼将居民分成两类:甲类(不参加体育锻炼)、乙类(参加体育锻炼),结果如下表:
甲类 | 乙类 | |
男性居民 | 3 | 15 |
女性居民 | 6 | 6 |
(Ⅰ)根据上表中的统计数据,完成下面的![]() 列联表;
列联表;
男性居民 | 女性居民 | 总计 | |
不参加体育锻炼 | |||
参加体育锻炼 | |||
总计 |
(Ⅱ)通过计算判断是否有90%的把握认为参加体育锻炼与否与性别有关?
附: ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.01 |
| 2.706 | 3.841 | 6.635 |