题目内容
某工厂家具车间造A、B型两类桌子,每张桌子需木工和漆工两道工序完成.已知木工做一张A、B型桌子分别需要1小时和2小时,漆工油漆一张A、B型桌子分别需要3小时和1小时;又知木工、漆工每天工作分别不得超过8小时和9小时,而工厂造一张A、B型桌子分别获利润2千元和3千元,试问工厂每天应生产A、B型桌子各多少张,才能获得利润最大?最大利润是多少?
每天应生产A型桌子2张,B型桌子3张才能获得最大利润,最大利润为13千元.
试题分析:设每天生产A型桌子x张,B型桌子y张,根据题意可列出不等式组

在平面直角坐标系中作出上不等式组所表示的平面区域,将目标函数
 化成
化成
当
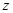 变化时,它表示一组平行直线,当该直线经过可行域且在
变化时,它表示一组平行直线,当该直线经过可行域且在 轴上的截距最大时
轴上的截距最大时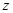 最大.依此找出最优解,求得
最大.依此找出最优解,求得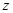 的最大值.
的最大值.试题解析:

解:设每天生产A型桌子x张,B型桌子y张,则

目标函数为:z=2x+3y
作出可行域:
把直线
 :2x+3y=0向右上方平移至
:2x+3y=0向右上方平移至 的位置时,直线经过可行域上的点M,且与原点距离最大,此时z=2x+3y取最大值
的位置时,直线经过可行域上的点M,且与原点距离最大,此时z=2x+3y取最大值解方程
 得M的坐标为(2,3)
得M的坐标为(2,3)此时最大利润
 千元
千元答:每天应生产A型桌子2张,B型桌子3张才能获得最大利润,最大利润为13千元.

练习册系列答案
相关题目
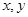 满足约束条件
满足约束条件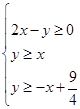 ,则
,则 的最小值为 .
的最小值为 .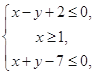 则
则 的取值范围是( )
的取值范围是( ) 


 ,(x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,则过这些点中的其中3个点可作不同的圆的个数为( )
,(x∈Z,y∈Z),每一对整数(x,y)对应平面上一个点,则过这些点中的其中3个点可作不同的圆的个数为( ) 在直线
在直线 的下方,则
的下方,则 的取值范围是_____________.
的取值范围是_____________. ,
, 满足
满足 时,
时, 恒成立,则实数
恒成立,则实数 的取值范围是________.
的取值范围是________.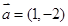 ,
,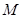 是平面区域
是平面区域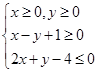 内的动点,
内的动点,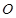 是坐标原点,则
是坐标原点,则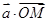 的最小值是 .
的最小值是 . 和
和 在直线
在直线 的两侧,则a的取值范围是( ).
的两侧,则a的取值范围是( ). 或
或
 或
或