题目内容
(本小题满分16分)
按照某学者的理论,假设一个人生产某产品单件成本为 元,如果他卖出该产品的单价为
元,如果他卖出该产品的单价为 元,则他的满意度为
元,则他的满意度为 ;如果他买进该产品的单价为
;如果他买进该产品的单价为 元,则他的满意度为
元,则他的满意度为 .如果一个人对两种交易(卖出或买进)的满意度分别为
.如果一个人对两种交易(卖出或买进)的满意度分别为 和
和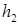 ,则他对这两种交易的综合满意度为
,则他对这两种交易的综合满意度为 .
.
现假设甲生产A、B两种产品的单件成本分别为12元和5元,乙生产A、B两种产品的单件成本分别为3元和20元,设产品A、B的单价分别为 元和
元和 元,甲买进A与卖出B的综合满意度为
元,甲买进A与卖出B的综合满意度为 ,乙卖出A与买进B的综合满意度为
,乙卖出A与买进B的综合满意度为
(1)求 和
和 关于
关于 、
、 的表达式;当
的表达式;当 时,求证:
时,求证: =
= ;
;
(2)设 ,当
,当 、
、 分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少? (3)记(2)中最大的综合满意度为
分别为多少时,甲、乙两人的综合满意度均最大?最大的综合满意度为多少? (3)记(2)中最大的综合满意度为 ,试问能否适当选取
,试问能否适当选取 、
、 的值,使得
的值,使得 和
和 同时成立,但等号不同时成立?试说明理由。
同时成立,但等号不同时成立?试说明理由。
【答案】
(2)即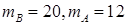 时,甲乙两人同时取到最大的综合满意度为
时,甲乙两人同时取到最大的综合满意度为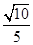 .
.
(3) 不存在满足条件的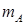 、
、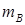 的值
的值
【解析】 本小题主要考查函数的概念、基本不等式等基础知识,考查数学建模能力、抽象概括能力以及数学阅读能力。满分16分。
(1) 
当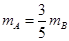 时,
时, ,
,
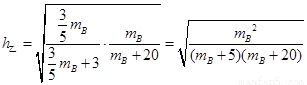 ,
, 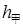 =
=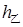
(2)当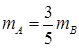 时,
时,
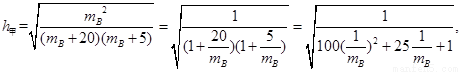
由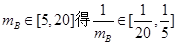 ,
,
故当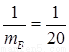 即
即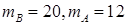 时,
时,
甲乙两人同时取到最大的综合满意度为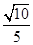 。
。
(3)(方法一)由(2)知: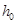 =
=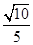
由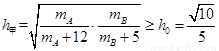 得:
得: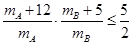 ,
,
令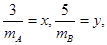 则
则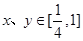 ,即:
,即: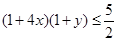 。
。
同理,由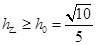 得:
得: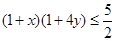
另一方面,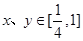
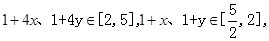
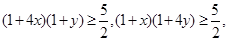 当且仅当
当且仅当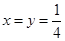 ,即
,即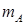 =
=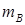 时,取等号。
时,取等号。
所以不能否适当选取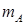 、
、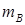 的值,使得
的值,使得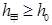 和
和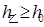 同时成立,但等号不同时成立。
同时成立,但等号不同时成立。


练习册系列答案
相关题目
 在平面直角坐标系
在平面直角坐标系 ,
, (
( ),
),
 ,对任意
,对任意 时,
时, 恒成立,求实数
恒成立,求实数 的范围;
的范围; ,当“
,当“ 在
在 的最大值.
的最大值. :方程
:方程 无实数根;
命题
无实数根;
命题 :函数
:函数 的值域是
的值域是 .如果命题
.如果命题 为真命题,
为真命题, 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围. 为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
 )的值;
)的值; 个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标延长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.